| Home Page |
Overview |
Site Map |
Index |
Appendix |
Illustration |
FAQ |
About |
Contact |
Elementary Particles
Contents
Quantum Domain
Elementary Particles
Fundamental Interactions
Unifications, A Brief History of Physics
Quantum Field Theory
Gauge Theory and the Standard Model
Asymptotic Freedom
Quark Confinement
Grand Unified Theory (GUT)
Supersymmetry
Superstrings
Manifold, Vacuum Energy, and Multiverse
Quantum Foam and Loop Quantum Gravity
Footnotes
References
Index
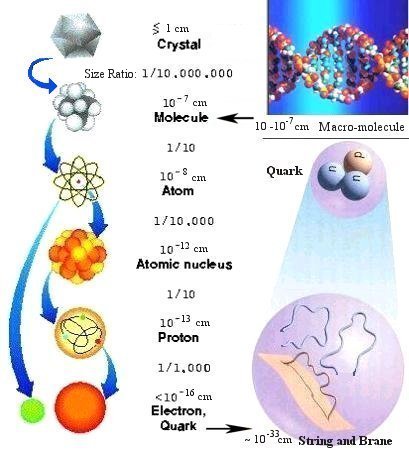 |
Figure 15-01 shows the size of those systems, which are governed by the rules in quantum theory. The deterministic property of classical physics is replaced by uncertainty for objects of such small size. Only the probability of certain quantities and processes can be estimated in this domain. It starts from molecule with a size of about 10-7cm to the hypothetical entity of string and membrane, which has a size of only 10-33cm. The size of the macro-molecules varies, the length of DNA can be up to 10 cm in human chromosom; while the width of the base pair is only 2x10-7 cm. The diagram also shows a proton composed of two up quarks and one down quark. According to the superstrings theory, these quarks are string or string attached to a membrane at the scale of less than 10-33cm, which is called the Planck scale - the smallest meaningful size (see Quantum Foam). Details about the instruments to probe the
|
|
elementary particle domain is presented in the appendix: "Particle Accelerators and Detectors".
|
[Top]
 |
 |
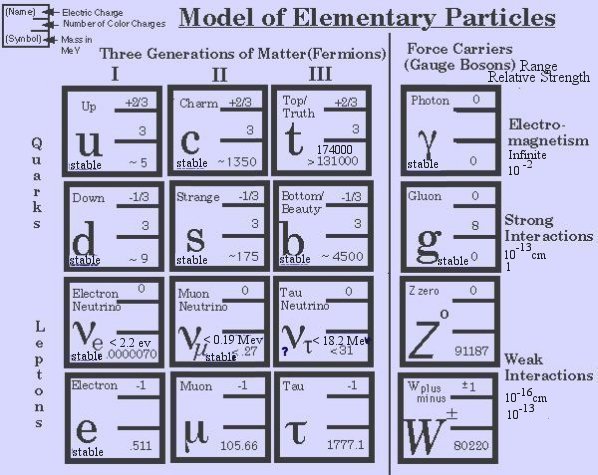
Although the table for elementary particles in Figure 15-02 is somewhat reminiscent to the periodic table discovered way back in 1869, it represents the cumulative efforts of theoretical and experimental research in physics over the last fifty years. The theore- tical frame work is more sophisticated and the experimental tools are highly complex
|
| |
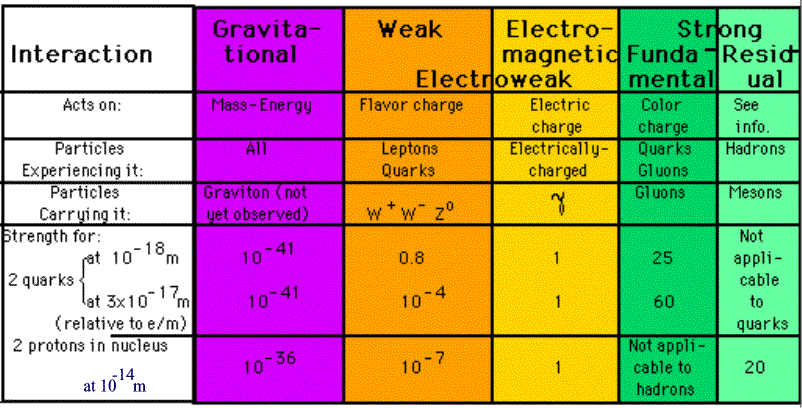
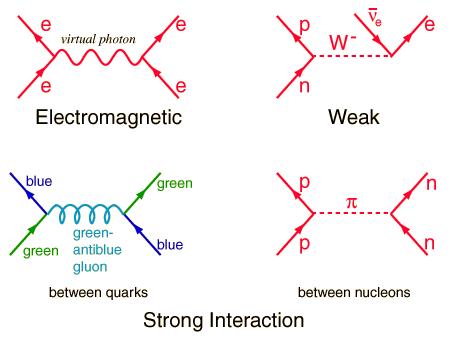
Figure 15-03 Fundamental Interactions [view large image] |
and expensive. Figure 15-03 lists the fundamental interactions, which take place between the various particles. To under- stand nature at its fundamental level we have to examine these two tables in details. |
- The mass of the particles are listed on the lower right-hand corner in unit of Mev. Some new data are added on top of the older ones if new experimental results are available. On the lower left-hand corner the member is labeled as stable or otherwise with blank space (Figure 15-04 is a pictorial view).
- Each member in the fermion generations has its own anti-particle with opposite electric charge and/or colour charge, e.g., the anti-particle of electron is the positron with one unit of positive charge and identical mass.
- The electric charge for quarks appears to be either -1/3 or 2/3. However, when three of them combine to form a baryon (fermion affected by strong interaction); it is always in such a way that the total charge is +2, +1, 0, or -1. When a quark and anti-quark combine to form a meson (boson affected by strong interaction); it is always in such a way that the total charge is +1, 0, or -1.
- Each quark can carry either one of the three varieties of colour charge -- red, green, and blue. This is just a label (a name) and has nothing to do with optics. In order to form a baryon the three quarks must each carry a different colour to add up to white. While in a meson the colour would be balanced by the anti-colour (such as red and anti-red).
- The force carriers are gauge bosons, which mediate the various kinds of interaction between the fermions. While photon does not carry electric charge, the gluons and the W bosons do carry colour charge, and electric charge respectively.
- The gauge bosons with mass are unstable. With just two exceptions, those elementary particles having mass over the range of Gev tend to be unstable.
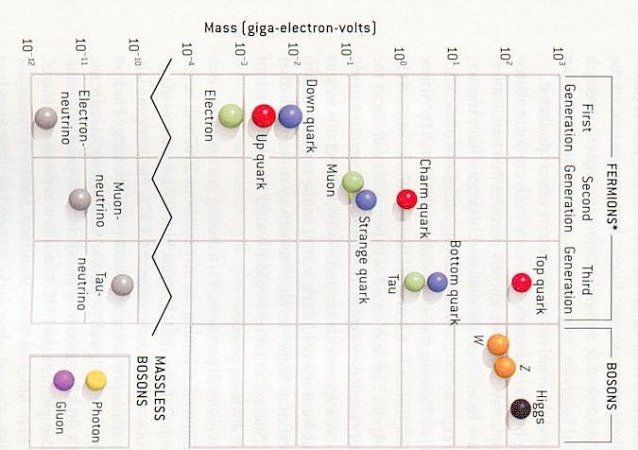 |
Figure 15-04 Elementary Particles (A Pictorial View)
[Top]
- There are four fundamental interactions act on the different charge carriers. These are the gravitational with mass-energy, the electromagnetic with electric charge, the weak and strong interactions with flavor and colour charges.
- The electromagnetic and weak interactions are unified at high energy into the electroweak interaction.
- The strong residual interaction is experienced by hardons (all the particles affected by the strong nuclear force) and generated by the quarks within. It is strong enough to overcome the electromagnetic repulsion between the hardons. This is similar to the Van der Waals force between molecules (except the difference in charge carrier). Note that most of the mass of nucleons (more than 90%) arises from the energy associated with the motion of the quarks and gluons that compose them - NOT from the rest mass of the constituents.
- The strengths of the various interactions in Figure 15-04 are relative to the electromagnetic interaction. It depends on the separation between the two particles. At a separation of 10-18 m. the electromagnetic and weak forces mixes to generate two new electroweak forces. According the the Grand Unified Theory (GUT), these electroweak forces merge with the strong force at 10-32 m.
- The strength for gravitational interaction is very weak at small separation. Its force carrier, the graviton, has not yet been detected. This interaction is poorly understood in domain of very small scale. One explanation relates the weakness of gravity to its leakage to other dimensions in a manyfold universe.
[Top]
 |
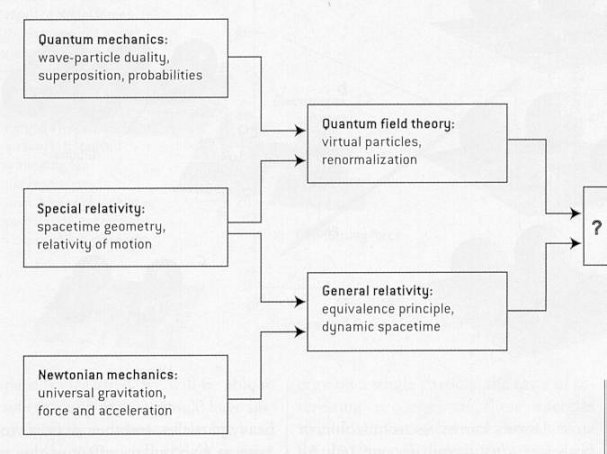 |
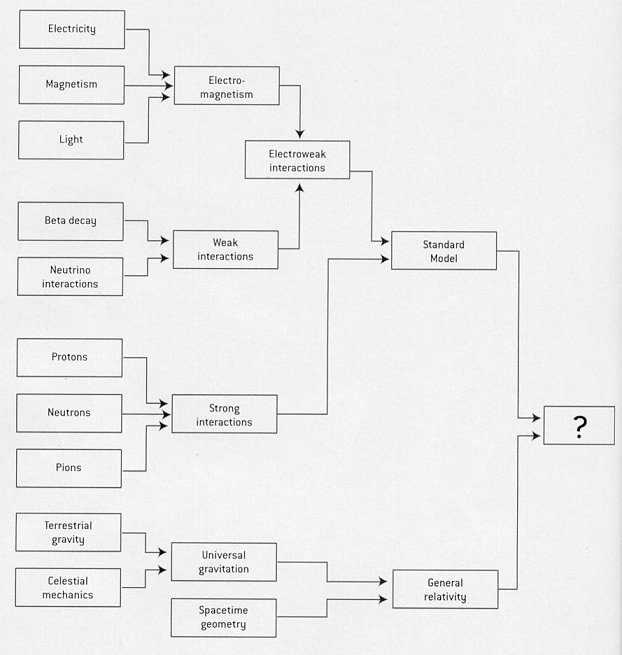
The history of physics is closely linked to the unification of seemingly disparate phenomena. (See Figure 15-05a.) Each stage of unification in turn advanced a new theoretical framework, which provides a deeper understanding of nature. (see Figure 15-05b.) The followings provides a history of the development of physics and the many unifications as depicted in Figure 15-05a. It also contains a brief description of the theoretical concept at each stage.
|
| |
|
|
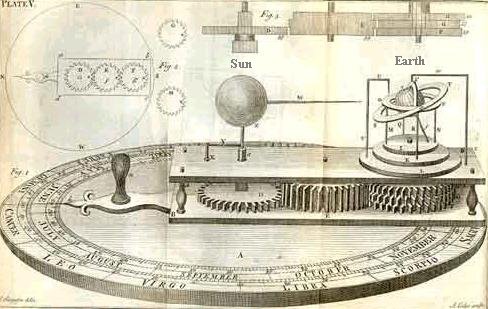
- Around 1680 Isaac Newton asserted that the force of "terrestrial" gravity (which makes apples fall to the ground, and which in Newton's view was a universal force) was the same as "celestial" gravity (the force which keeps planets in motion around the Sun, see Figure 15-05c). Such a force is long-range. Its effects can be felt at any distance, though attenuated by the square of the distance between the two "gravitating" objects concerned. Newton introduced a new
 |
fundamental constant of nature, G, which characterizes the strength of the gravitational force. Gravity is always attractive in contrast to other forces of nature. Newtonian mechanics works in a three dimensional Euclid space (flat space). Time is independent of the system of reference -- it is just a running variable. An invariance in such space is the length. It is the same in any inertial frames of reference. Other consequences derived from Newton's formalism include action at a distance, i.e., there is no time delay for the two "gravitating" objects to interact; and determinism, which assumes that events are entirely determined by other, earlier events.
|
| |
|
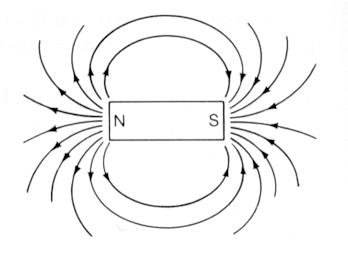 |
- The electric and magnetic fields (Figure 15-05d) were described in terms of the Coulomb's Law (about charge and electric field), the Ampere's Law (about current and magnetic field), and the Faraday's Law (a relationship between electric and magnetic fields). Faraday's observation has inspired J. C. Maxwell to assemble these laws into a consistent set of equations in 1865 and is now known as Maxwell's equations. The disturbance of the electromagnetic fields was subsequently identified as the light wave in optics
|
| |
|
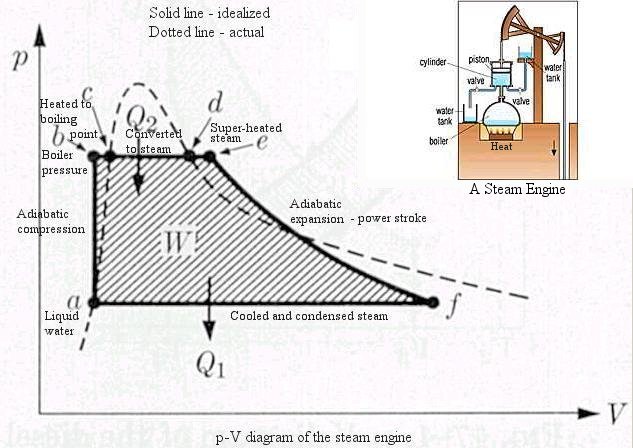 |
- Thermodynamics is a branch of physcis developed in the 19th century. It began with the invention of the steam engine (Figure 15-05e) at the beginning of the industrial revolution. It was driven by the need to have a better source and more efficient use of energy than the competitors (among English, French, and German). It was a case where technology drove basic research rather than vice versa. Thermodynamics provides a macroscopic description of matter and energy. Today better insight is obtained by linking the subject with the statistical behaviour of microscopic particles.
|
| |
|
- In 1887 Michelson and Morley showed conclusively that the velocity of light is constant in all inertial1 systems of reference. This observation led Einstein to propose the principle of relativity in 1905. This is also known as the Special Theory of Relativity, which treats space and time on an equal footing such that the velocity of light is constant in this four dimensional space-time. It implies that space and time can transform among each other in different inertial systems
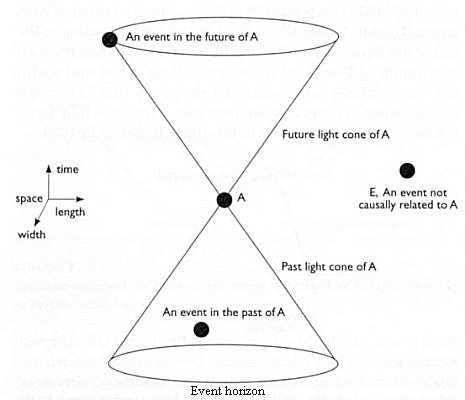 |
of reference. In particular, time ticks slower and length becomes shorter in a fast moving reference frame (with respect to the observer). Another consequence is the finite propagation of interaction, the signal can travel from the past to object A only with a speed less than or equal to the velocity of light. The light cones in Figure 15-05f define the space within which communication is possible. They form the event horizons for a particular time in the past or future. These ideas are in complete variance with the Newtonian Mechanics. However, classical mechanics is still a good approximation for phenomena involving low velocity (in comparing to the velocity of light).
|
| |
|
 |
- Starting from the principle of equivalence (Figure 15-05g), which states that the properties of the motion in a free falling non-inertial (accelerating) system in the presence of a gravitational field is the same as those in an inertial (non-accelerating) system , Einstein proposed the General Theory of Relativity in 1915. In general relativity, it is postulated that the curvature of space-time determines gravity. The mass-energy generates the curvature of space-time and particles moving along the geodesic in this four dimensional curved space. The geodesic is the shortest distance between two points. It is a straight line only in Euclidean space (flat space); it would be different in the curved space (Riemann space).
|
Figure 15-05g Principle of Equivalence |
|
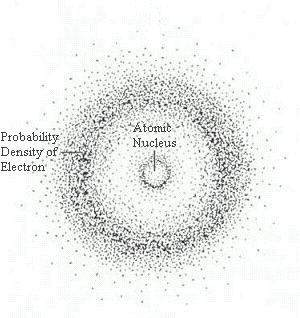 |
- Quantum theory was developed in 1925-1926 by Erwin Schrodinger, Werner Heisenberg, and others in response to many inconsistences between expermental data and classical theories. The first difference between classical and quantum theories is that whereas classical theory always deals with continuously varying quantities, quantum theory must also deals with discontinuous or indivisible processes. The second difference is that whereas classical theory completely determines the relationship between variables at an elarlier time and those at a later time, quantum laws determine only probabilities (Figure 15-05h) of future events in terms of given conditions in the past. By the early 1930s the application of quantum theory to problems involving nuclei, atoms, molecules, and matter in the solid state made it possible to understand a vast body of otherwise-puzzling data and led to predictions of remarkable accuracy.
|
| |
|
- Beta decay was a main topic of research in the first decades of the 20th century. It was found that the electrons produced in the decay has energy always less than the 1.5 me available when the neutron transmutes into a proton. It was Wolfgang Pauli who came up with the answer in 1930. He surmised that there must be another particle running away with the "missing energy". The particle required to do the job must have zero mass and no electric charge to
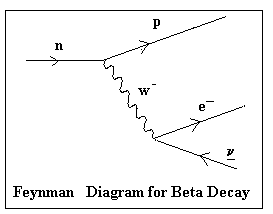 |
escape detection by the experimenters. In 1933 Enrico Fermi took up Pauli's idea and put it on a respectable footing by introducing a new force called "weak" interaction. The hypothetical particle is called neutrino. He proposed that when a neutron changes into a proton it emits a mediating boson called W-, which carries off the negative electric charge and excess energy, while the neutron changes into a proton and recoils. The W- boson then quickly decays into an electron and an anti-neutrino (see Figure 15-05i). Evidence for the existence of the neutrino came in 1953. The W- boson was discovered in 1983. |
| |
|
- It was well aware in the 1930s that the force that hold the neutrons and protons together in the nucleus has to be short-range, extending only over about the diameter of a nucleus, otherwise it would pull all the other nuclei together. In 1935 Hideki Yukawa suggested that the strong nuclear force (Figure 15-05j) must be mediated by the exchange of another
 |
kind of force-carrying particle, which became known as pion. His explanation for the short range of the force is related to the uncertainty principle. If the pion has mass, then its virtual existence can last only for a short time. He estimated the mass of the pion to be 150 Mev. The actual mass is 140 Mev when it was discovered in 1947. It is now known that the pion is a composite boson, it is not truly a fundamental force carrier. |
| |
|
- While the quantization of particles is adequte for low energy phemonena in molecules and atoms, the quantization of fields is more appropriate for high energy particles involving creation and annihilation. Such theoretical frame work is called quantum field theory, in which matters are represented by fermion fields and the interactions are mediated by gauge bosons. The interaction of electromagnetic and electron fields was the first treated by such kind of formulism, and known as quantum electrodynamics (QED). It was developed by Richard Feynman, Julian Schwinger and others in the late 1940s. QED makes predictions about the scattering of photons and electrons and other charged particles that agree with experiment to an accuracy of eleven decimal places. All the computations are perfromed by a procedure called perturbation theory, which seems to be very promising for small coupling constant. Each term in the perturbative series can be represented by a graph known as Feynman diagram (Figure 15-05k). The K+ and
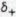 factors in the mathematical expression represent the probobility amplitude of the process between points (s56 is the distance travels by the photon). At the vertex (intersection), the likelihood that an electron would emit or absorb a photon is e
factors in the mathematical expression represent the probobility amplitude of the process between points (s56 is the distance travels by the photon). At the vertex (intersection), the likelihood that an electron would emit or absorb a photon is e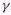
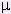 , where e is the electron's charge and
, where e is the electron's charge and 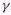
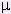 a vector called Dirac matrices to keep track of the electron's spin. Conversely, a process can be computed by drawing graphs and then applying the Feynman rules. The trouble with Feynman's method is that it always leads to infinite expressions for the loop diagrams such as those in the fourth order electron-electron scattering (diagrams a - i in Figure 15-05k). However, Feynman and others discovered that these are related only
a vector called Dirac matrices to keep track of the electron's spin. Conversely, a process can be computed by drawing graphs and then applying the Feynman rules. The trouble with Feynman's method is that it always leads to infinite expressions for the loop diagrams such as those in the fourth order electron-electron scattering (diagrams a - i in Figure 15-05k). However, Feynman and others discovered that these are related only
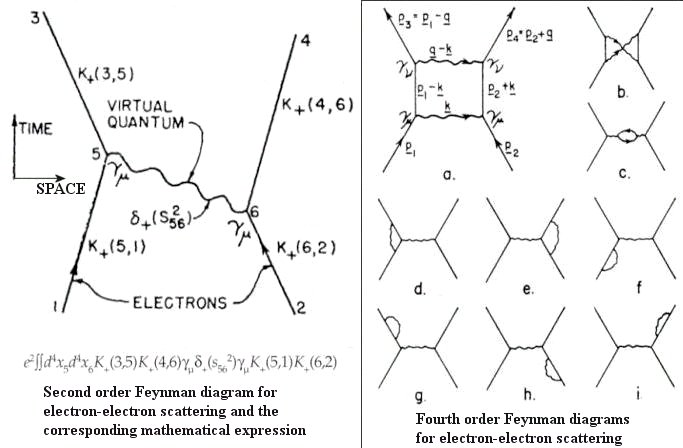 |
to quantities involving mass and charge. It is then figured out that if one simply corsses out these infinite answeres wherever they appear, and substitutes the right, finite answer, all the calculations become sensible again. This procedure is called renormalization. When it works for a theory, that theory is said to be renormalizable. The electroweak interaction and quantum chromo-dynamics are the other examples of renormalizable theory. Unfortunately, quantum gravity is not renoramlizable. New theories are being developed to allow the merger of quantum theroy and the gravitational force. |
| |
|
- Parity is the operation P that reverses the coordinate (x,y,z) to (-x,-y,-z) of a system (e.g., a particle or collection of particles). It is equivalent to a mirror reflection followed by a rotation through 180o. The parity can be +1 or -1 for a system depending on whether the corresponding field remains the same or flips a sign, i.e., in simple mathematical expression: P
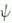 (x,t) =
(x,t) = 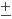
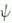 (-x,t). The overall parity is given by the multiplication of its parts, e.g. (+1)x(-1)x(+1) = (-1) etc. It has been long held that parity is conserved before and after all particle interactions. The processes in which parity is not conserved would look different in the mirror image (+ 180o rotation) world. With some hints from experimental
(-x,t). The overall parity is given by the multiplication of its parts, e.g. (+1)x(-1)x(+1) = (-1) etc. It has been long held that parity is conserved before and after all particle interactions. The processes in which parity is not conserved would look different in the mirror image (+ 180o rotation) world. With some hints from experimental
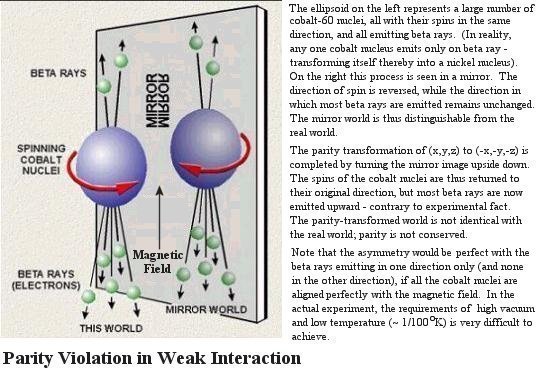 |
results, T. D. Lee and C. N. Yang pointed out that conservation of parity may be violated in weak interaction. A test was arranged by C. S. Wu to observe the beta decay of cobalt-60 in a magnetic field. It shows a preferred direction for the emitting electrons (the left-handed electrons) and thus validates the hypothesis of parity violation for weak interaction -- the mirror world behaves differently from the real world (see Figure 15-05l). The three Chinese physicists shared the 1957 Nobel Prize for their efforts in identifying this peculiar behaviour in weak interaction. |
| |
Note that parity will be conserved if there are equal number of electrons in both directions. It is a useful tool to predict permissible process when parity is conserved.
|
- One of the greatest triumphs of theoretical physics in the second half of the 20th century was the discovery, made independently by Abdus Salam and by Steven Weinberg in 1967, of a way to describe the weak interaction and the
 |
electromagnetic interaction in one mathematical formalism, as a single force - the electroweak interaction (based in part on work developed previously by Sheldon Glashow). The theory requires three intermediate vector bosons with mass to explain the weak interaction. The predicted masses of these bosons were duly observed in experiments at CERN in the early 1980s. A scalar (spin 0) field called the Higgs field is introduced in this formalism to endow mass to the gauge bosons Zo, W+, and W-. The lower limit on the mass of the Higgs boson is estimated to be 113 Gev. At present, there is no experimental evidence in favor of a Higgs boson, nor is there any against. Figure 15-05m shows the Feynman diagrams for interactions in the Standard model including the electromagnetic and weak interaction. |
Figure 15-05m Interactions in Standard Model
[view large image] |
|
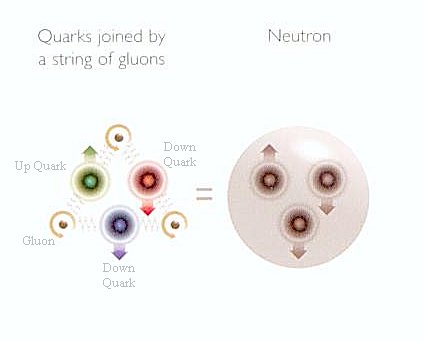 |
- A similar formalism was developed for the strong interaction in the 1970s. The story starts with three doublets of quark flavors (u, d), (c, s) and (t, b) (See Figure 15-03). It turns out that there are not just six but eighteen distinct quarks, distinguished from each other by colour charge. Each quark comes in three colour charges -- red, green, and blue. The gauge symmetry between these three colour charges give rise to eight gauge bosons -- called gluons, which remain massless (no Higgs field interaction is necessary). Detailed tests have supported the idea of the strong interaction being mediated by the gluons. This formalism is called Quantum Chromodynamics (QCD). For example, the neutron is a combination of two down
|
| |
quarks and one up quark bound by gluons to form a white composite particle (Figure 15-05n). Together, the electroweak theory and QCD constitute what has become known as the "Standard Model" of elementary particles. |
- General relativity and quantum theory describe two extreme of physics - the former is on the very large scale up to the whole universe, while the latter is on the smallest possible scale down to the size of elementary particles. However, there are many instances in which both general relativity and quantum theory are equally important and a common framework is essential. One obvious such instance is in the very early universe, immediately after the Big Bang (Figure 15-05o), when the size is very small and the curvature of space-time were nearly infinite. Much of the difficulty in merging these
 |
 |
theories comes from the radically different assumptions that these theories make on how the universe works. Quantum field theory depends on particle fields embedded in a fixed flat space-time, while general relativity models gravity as space-time curvature that changes as mass moves. The most obvious ways of combining the two (such as treating gravity as simply another particle field) run quickly into problem of infinite Feynman diagrams. Currently, there are three roads leading to the domain of qunatum gravity:
|
|
|
|
- Hawking Radiation - By combining the uncertainty principle in quantum theroy and the general relativity concept of black holes, Stephen Hawking showed that black holes are not completely black, but would actually radiate. As a bonus, he also found new connections between gravity and thermodynamics, i.e., entropy (and hence information) is equal to 1/4 of the area (in Planck units) of the black hole's event horizon. Thus, the amount of information that can be contained in that region is finite. This implies that the world must be discrete on the Planck scale, for were it continuous any region could contain an infinite amount of information. See Hawking Radiation, Relativity in the appendix for more details.
- Superstring theory - It started out as a generalization of quantum field theory where instead of point particles, string-like objects (with size ~ the Planck length = 10-33 cm) propagate in a fixed spacetime background. Although string theory had its origins in the study of quark confinement and not of quantum gravity, it was soon discovered that the string spectrum contains the graviton, and that "condensation" of certain vibration modes of strings is equivalent to a modification of the original background. It is suggested that in the "yet to be formulated" fundamental superstring theory such as the M theory, the background dependent apporach should be replaced by a scheme involving dynamic space time. See section on "Superstrings" for more details.
- Loop Quantum Gravity - One reason why it has taken so long to construct a quantum theory of gravity is that all previous quantum theories were background dependent. The problem of how to build a quantum theoretic description of a world in which space and time are nothing but networks of relationships was solved only 20 years ago in the 1980s. The relational theory that resulted is called loop quantum gravity. According to this theory, space is made of discrete units in size of the Planck length. In contrast to ordinary geometry, a given region cannot have a volume which is arbitrarily big or small - instead, the volume must be one of a finite set of numbers (similar to some of the quantized quantities in quantum theory). Similarly, time is also made of discrete units called the Planck time (10-43 sec). The theory offers more than a picture: it makes precise predictions about what would be observed were it possible to probe the geometry of space at distances as short as the Planck scale. See section on "Quantum Foam and Loop Quantum Gravity" for more details.
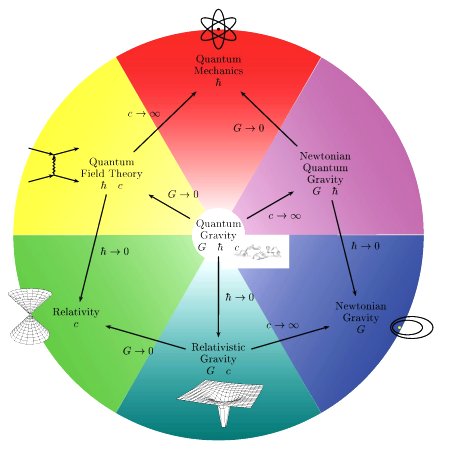
A few of the other approaches to quantum gravity will turn out to play significant roles in the final synthesis. Among them will be the twistor theory and the non-commutative geometry. They will provide essential insights into the nature of the quantum geometry of space-time. Quantum gravity will emerge as a more fundamental theory since it will possess more explanatory and predictive powers. Figure 15-05p shows the relationship between quantum gravity and the other branches of physics at the limit of the various universal constants, where the gravitational constant G is associated with gravity, the Planck constant 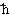 is for quantum, and the velocity of light c comes with special relativity. In quantum gravity, all the fundamental units are expressed in terms of G,
is for quantum, and the velocity of light c comes with special relativity. In quantum gravity, all the fundamental units are expressed in terms of G, 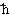 , and c: Planck length = (G
, and c: Planck length = (G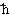 /c3)1/2 = 1.62x10-33 cm, Planck time = (G
/c3)1/2 = 1.62x10-33 cm, Planck time = (G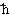 /c5)1/2 = 5.39x10-44 sec, Planck mass = (
/c5)1/2 = 5.39x10-44 sec, Planck mass = (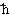 c/G)1/2 = 2.17x10-5 gm, Planck energy = (
c/G)1/2 = 2.17x10-5 gm, Planck energy = (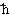 c5/G)1/2 = 1.22x1019 Gev, and Planck temperature = (
c5/G)1/2 = 1.22x1019 Gev, and Planck temperature = (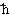 c5/GkB2)1/2 = 1.42x1032 oK, where kB is the Boltzmann's constant, which relates energy to absolute temperature on the Kelvin scale.
c5/GkB2)1/2 = 1.42x1032 oK, where kB is the Boltzmann's constant, which relates energy to absolute temperature on the Kelvin scale.
[Top]
Quantum Field Theory
It has been mentioned in Topic 12 that the transition from classical to quantum mechanics can be accomplished either by the path integral method or by the more ad hoc "canonical quantization" such that the momentum p and position q are no longer mere numbers but are operator satisfying the commutative relation: pq - qp ~ 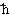 . The Schrodinger equation was developed and applied to the atomic and molecular system with great success. This formalism becomes increasingly inaccurate for phenomena in smaller domain where energy can manifest itself in a variety of ways, e.g., pair creation or particle moving at relativistic speed. Therefore, the Schrodinger equation has to be replaced by field equations such as the Klein-Gordon equation (for particle with no spin) or Dirac equation (for particle with spin 1/2). These field equations are invariant (unchanged) under a change of the space-time coordinate system (Lorentz transformation). It is referred to as relativistic invariance, which ensures the validity of the field equation at relativistic speed. To account for the creation/annihilation of particles in high energy interaction, the field is considered to be an operator. It is expanded into Fourier series in terms of harmonic functions and coefficients. These coefficients are then subjected to some quantization rules. Depending on whether the particle has integer or half integer spin, these operators satisfy the commutation or anti-commutation relations (for example: ab + ba = 1; the Pauli exclusion principle is guaranteed by quantization with the anti-commutation relations for spin 1/2 particles). They are the creation and annihilation operators, which operate on state vectors describing the number of particles in different states. This is called the second quantization, which endows particle property to the field (field + second quantization = quantum field). Thus, in quantum field theory the particles are just bundles of energy and momentum of the fields, which constitute the basic ingredient. A more mathematically oriented description on Quantum Field Theory can be found in the appendix.
. The Schrodinger equation was developed and applied to the atomic and molecular system with great success. This formalism becomes increasingly inaccurate for phenomena in smaller domain where energy can manifest itself in a variety of ways, e.g., pair creation or particle moving at relativistic speed. Therefore, the Schrodinger equation has to be replaced by field equations such as the Klein-Gordon equation (for particle with no spin) or Dirac equation (for particle with spin 1/2). These field equations are invariant (unchanged) under a change of the space-time coordinate system (Lorentz transformation). It is referred to as relativistic invariance, which ensures the validity of the field equation at relativistic speed. To account for the creation/annihilation of particles in high energy interaction, the field is considered to be an operator. It is expanded into Fourier series in terms of harmonic functions and coefficients. These coefficients are then subjected to some quantization rules. Depending on whether the particle has integer or half integer spin, these operators satisfy the commutation or anti-commutation relations (for example: ab + ba = 1; the Pauli exclusion principle is guaranteed by quantization with the anti-commutation relations for spin 1/2 particles). They are the creation and annihilation operators, which operate on state vectors describing the number of particles in different states. This is called the second quantization, which endows particle property to the field (field + second quantization = quantum field). Thus, in quantum field theory the particles are just bundles of energy and momentum of the fields, which constitute the basic ingredient. A more mathematically oriented description on Quantum Field Theory can be found in the appendix.
Before performing the second quantization, a field equation has to be available to describe the dynamic of the field. It is found that the field equation is equivalent to minimizing the "Action", which is now a function of the field and its first derivative. Since there is an infinite choice for the form of the "Action", some conditions are imposed to limit the arbitrariness. For example, the "Action" should be invariant (unchanged) under the operation of translation, rotation, and time progression (these kinds of symmetry imply the conservation of momentum, angular momentum, and mass-energy respectively). However, the symmetry of the "Action" or the field equation does not guarantee the same for its solution. For example, the Schrodinger Equation (mentioned in topic 12) have rotational symmetry for the hydrogen atom, and yet only the wave function corresponding to zero angular momentum possesses a spherical configuration. (See Figure 12-07.)
[Top]
The modern theory of elementary particles depends heavily on the concept of gauge invariance, which was used to describe some global changes that do not have any effect on observation. For example, if the electric voltage throughout the circuit is raised uniformly by the same amount, there would not be any observable effect. But locally at a specific space and time, when a disturbance happens to a fermion field for example, something will react to restore the original "appearance". That something turns out to be the gauge bosons mentioned earlier in Figure 15-03. For example, in the electromagnetic interaction a local disturbance can be considered as a two dimensional rotation of the quantum field (which is usually a complex function2) in an "internal space". The photon (the gauge boson) is the response to restore the "appearance" (see Figure 15-06a), which signifies mathematically the invariance of the "Action" with this internal rotation. Theoretical physicists are fond of putting similar objects
 |
together called a group. For the case of electromagnetic interaction, there is only one kind of objects -- the two dimensional internal rotation. The different rotational displacements form a group, this particular group is called U(1). The symbol U indicates that the transformation (the internal rotation) is unitary, which preserves the normalization (probability). This
U(1) group has the property that the internal rotation operations are commutative -- mathematicians call such kind of group an Abelian group. Similar gauge invariances exist for the strong and weak interactions, the "internal rotation" depends on more than one parameter in these cases. Group of objects can be formed from these generalized "rotational displacements". However, these elements are no longer commutative. Such groups are called non-Abelian. The gauge theory for the U(1) is called Quantum Electrodynamics (QED).
|
| |
|
The non-Abelian group called SU(2) is applicable to the case of weak interaction. The internal rotation is generalized to three parameters corresponding to three different gauge bosons -- W+, W-, and Z0. The participating particles are the left-handed3 pair of leptons. In the Weinberg-Salam model, the left-handed leptons can undergo both electromagnetic and weak interactions while the right-handed electron can only participate in electronmagnetic interaction. Thus the model unifies these two interactions. This asymmetry in chirality is related to the phenomenon of parity violation4 in weak interaction, and has been verified conclusively in the 1950s. The electroweak unification occurs at energy above 102 Gev. A complication arises with regards to the mass of gauge bosons for which, the original Yang-Mills theory4 failed to account for.
 |
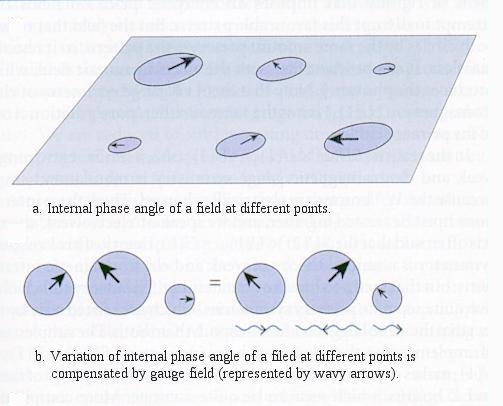
In superconductivity, it is known that the Meissner effect, where the magnetic field is expelled from the superconducting material, can be interpreted as the electromagnetic field (the photon) acquiring mass while trying to disrupt the ordered structure of the Copper pairs (see Figure 15-06b). But the gauge bosons in weak interaction have mass even in empty space. Since no form of matter identified so far provides a suitable candidate, we are therefore led to
|
| |
postualate that there is a new form of matter doing the job. Accordingly, what we perceive as empty space is in fact filled with an exotic, suitably aligned substrate: the Higgs condensate. |
In the mathematical formalism, these Higgs fields are added to the "Action" for the electroweak interaction. At the transition temperature (happened early in the Big Bang), these Higgs fields5 move to more stable states in lower energy level. However,
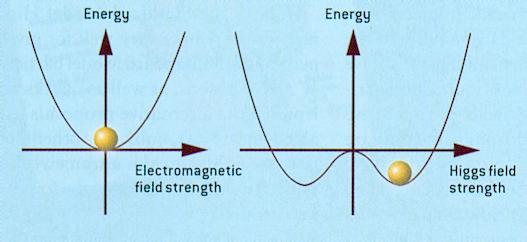 |
unlike the electromagnetic field, which has its minimum energy at zero field strength; the Higgs field, in contrast, has its minimum energy at a nonzero field strength (see Figure 15-06c, in this diagram the "ball" represents the preferred state of the universe). Thus, the universe, in its natural lowest energy state, is permeated by that nonzero value of the Higgs field. Once this happens, all the particles (both bosons and fermions) would acquire mass by interacting with the Higgs field. There is now a convincing consensus of experimental results supporting this electroweak theory.
|
| |
|
When the internal rotation is generalized to SU(3), The gauge theory can be applied to the case of strong interaction. There are eight parameters for this group corresponding to eight gauge bosons called gluons. The participating particles are the quarks with 3 different colour charges -- red (r), green (g), and blue (b). Three quarks with different colour charges combine to form a baryon. Each quark can carry different colour charges at different time, provided the colour combination is "white". Unlike the case of the U(1) group where the gauge boson (the photon) does not carry charge, the gluons do themselves carry the colour charges. Such difference produces phenomenon such as asymptotic freedom and quark confinement. The gauge theory for the SU(3) group is called Quantum Chromodynamics (QCD). The formulism for QCD and electroweak interaction together is known as the Standard Model, which describes all the phenomena associated with leptons and quarks.
[Top]
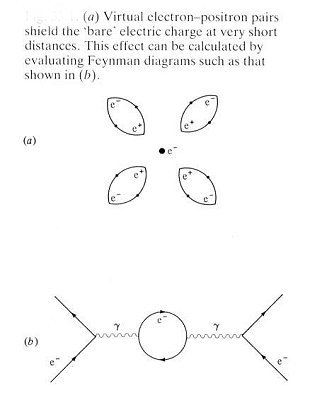 |
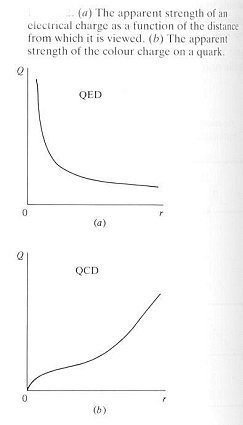 |
In electromagnetic interaction the Coulomb's inverse square law becomes increasingly inadequate at small separation between the two charges because they begin to penetrate the virtual electron-positron shield as shown in part (a) of Figure 15-07 and 15-08. A parallel phenomenon exists in strong interaction. However, there is the additional virtual gluon shielding, which has the opposite effect and produce the apparent strength of the colour charge as shown in part (b) of Figure 15-08. It shows that the interaction strength falls off with decreasing separation. At very small separation the quarks appear as free -- not interacting with each other. Thus at small separation, the methods of perturbation theory is applicable again to calculate quantities of physical interest.
|
| |
|
|
[Top]
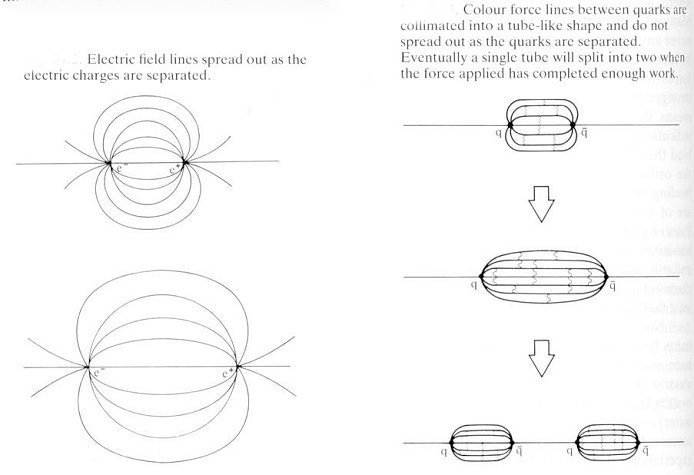 |
In electromagnetic interaction, the electric field lines spread out when the charges move away from each other as shown in the left diagram of Figure 15-09. The same situation in QCD elicits a different response because the gluons themselves also carry the colour charges. The field lines (of the moving sources) are drawn together by the mutual attraction instead of spreading out. (See right diagram of Figure 15-09.) As the pull getting stronger with further separation, the system will gain enough energy to promote a virtual quark-antiquark pair from the vacuum into physical reality. This will give rise to the creation of a new meson as shown in the right-bottom diagram of Figure 15-09. So the energy expended in attempting to separate the quarks has resulted in the production of another meson, no free quark is produced.
|
| |
|
[Top]
Although the Standard Model has been very successful in accounting for all experimental phenomena, it is not expected to be the ultimate theory because of its great complexity and the many questions it leaves unanswered. These objections seem to suggest that there may be deeper symmetries underlying the standard model, leading perhaps to the unification of the strong and electroweak interactions into a single "Grand Unified theory", or GUT. Such scheme is indeed possible if the internal rotation group is further generalized to SU(5) with 24 parameters. All the elementary particles are assigned into
 |
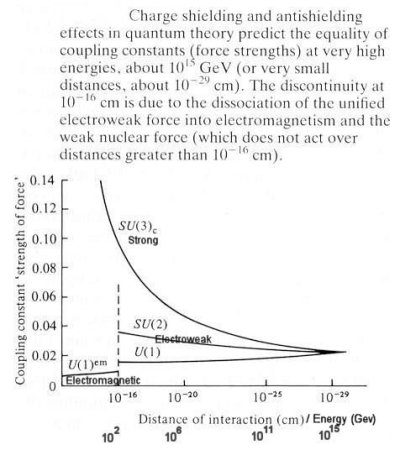 |
two 5-multiplets and two 10-multiplets. Figure 15-10 shows one of the 5-multiplets with the 24 gauge bosons assignment arranged into a matrix. Of these, 12 are familiar (the photon, W+, W-, Z0 and 8 gluons). The remaining 12 are new bosons denoted by X; these carry new forces which can transform quarks into leptons and vice versa. The mass of the X bosons have been calculated under the Higgs mechanism, and turns out to be about 1015 Gev. These super-heavy particles lie many orders of magnitude beyond the energy ranges of any conceivable accelerator. However, they would be present in great abundance in the first 10-35 sec after the Big Bang. |
| |
|
|
At energies well above 1015 Gev, all gauge bosons (including the Xs) can be produced freely and all interactions have the same strength and quarks can transform into leptons as easily as they change colours; and the grand SU(5) symmetry is manifest. At an energy of about 1015 Gev, the SU(5) symmetry breaks down to separate SU(3) and SU(2)XU(1) symmetries and the grand unified interaction separates into the strong and electroweak interactions. At about 102 Gev, the SU(2)XU(1) symmetry becomes broken, reflecting the separation of electroweak interaction into the distinct weak and electromagnetic interactions.
This picture of the unification of interactions also incorporates the variation in the strengths of charges, depending on the distance from which they are acted upon as shown in Figure 15-11. The most dramatic consequence of grand unification is that the proton is no longer stable, it has a small probability for decay into a neutral pion and a positron (with a half life of about 1032 years). No such decay has been detected so far.
[Top]
Supersymmetry differs from all other symmetries in that it relates two classes of elementary particles which are so fundamentally different -- the fermions and the bosons. According to supersymmetry, every "ordinary" particle has a companion particle -- differing in spin by half a unit, but with otherwise identical properties. Furthermore, the strengths of the interactions of the superpartners are identical to those of the corresponding ordinary particle.
 |
The last column in Figure 15-12 shows the names and symbols for all the superpartners -- "s" in front of the fermion superpartner, "ion" behind the boson superpartner, and a "~" on the top of a symbol to designate the superpartner.
As mentioned in the GUT, the X particles have mass of the order 1015 Gev, while electroweak bosons have mass of the order 102 Gev. This huge difference in mass requires fine tune of numerical parameters to better than one part in 1012, and is often referred to as the "hierarchy problem". Supersymmetry, however, leads to delicate cancellations in the computation of these masses in an entirely natural way. Hence, the enormous difference between the electroweak scale and GUT scale is an uncontrived feature of supersymmetric models, i.e., supersymmetry provides an explanation.
Another motivation for supersymmetry is its intimate connection with gravity. If supersymmetry is promoted to a local gauge symmetry, then the theory automatically incorporates Einstein's theory of general relativity. Theories with local supersymmetry are called super-gravity theories. Although such attempts to merge general relativity with quantum mechanics ultimately met with failure, the more promising application is associated with ten dimensional string theories. Super-gravity is the low energy limit where the structureless point particle
|
| |
|
is a good approximation. Supersymmetry also addresses a host of other mysteries in modern physics such as the tremendous concentration of energy in the universe (the cosmological constant problem), the origin of cosmic inflation, matter/antimatter asymmetry, the nature of cold dark matter, and the special forms of the Higgs interactions.
If supersymmetry were an exact, unbroken symmetry, the superpartners would have the same mass of the ordinary particles. However, no such particles have ever been observed, and supersymmetry, therefore, if it is a true symmetry of particle physics, must be broken. If the breaking of supersymmetry is in such a way that the explanation for the hierarchy problem is still valid, then the mass of the superpartners would be in the order of 103 Gev -- just at the mass range accessible to the new generation of accelerators.
[Top]
According to the theory of superstrings, the fundamental constituents of the material world are not point-like elementary particles, but tiny one-dimensional strings having a length of about 10-33 cm (the Planck length). Like the string of a violin, they can vibrate in many different ways (different modes), which correspond to the different elementary particles observed in nature. It is a quantum theory that incorporates gravity naturally. In its larger framework of M-theory, the strengths of all the four fundamental forces merge together at very small distance (~10-33 cm.) as shown in Figure 15-13.
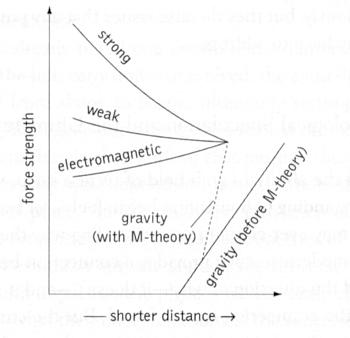 |
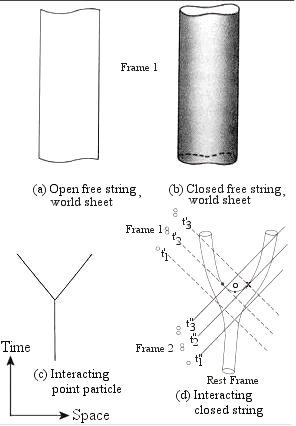 |
There are two classes of strings, those with ends (open strings), and those without (closed strings -- a loop) as shown in Figure 15-14(a) and (b). The particles associated with the open strings are the spin-1 gauge bosons and fermions. Their movement is restricted on the surface of a membrane by some boundary conditions. Graviton with spin-2 is an example of closed string, which can travel freely in all spatial dimensions. These are the ingredients for the theory of manyfold universe. When a point particle moves through space-time, it follows a geodesic (a path of minimum length) and sweeps out a one-dimensional curve which is referred to as its world-line (Figure
|
| |
|
15-14(c)). However, when a string propagates through space-time, it sweeps out a two-dimensional surface which, by analogy, is called its world-sheet, and moves along a surface of minimum area. (See |
Figure 15-14(a) and(b)). Figure 15-14(c) shows a point particle splits into two. Since the vertex is a point, there are many possible forms of interaction, all of which are invariant under the Lorentz transformation. However, when a string splits into two as shown in Figure 15-14(d), there is no well-defined notion of when and where this happened. For example, the string splits at point o in the rest frame, in inertial frame 1, the splitting occurred at the point indicated with the solid dot, and for inertial frame 2, it is at the point indicated with the cross. As a result there is only one choice for the interaction. All the other inertial frames have to follow the same rule.
When supersymmetry is incorporated into the original string theory, it resolves the problem with tachyon (square of mass is negative), accommodates the ferminonic vibrational pattern, and merge general relativity with quantum mechanics. The Theory of Strings becomes the Theory of Superstrings.
The "heterotic" superstring theory is a theory of closed strings. In contrast to open strings with gauge charges at the endpoints, here the gauge charges are "smeared" over the entire heterotic string. Vibrations (waves) can travel around any closed string in two directions, but the unusual feature of the heterotic string is that the waves moving in each direction are completely different. The clockwise moving waves are the waves of the 10-dimensional superstring, whereas the waves moving anticlockwise are those of the original 26-dimensional bosonic string. To obtain a consistent 10 dimensional theory, 16 of the extra dimensions are interpreted as internal degrees of freedom, which are found to be related to local gauge symmetry.
 |
 |
A ten-dimensional space is required in order to eliminate ghosts (negative probability) in the formalism. To specify a point in this 10-dimensional space requires the usual four (x, y, z, t), plus an additional six more coordinates. Suppose one of these extra coordinates is curled into a small circle,
|
| |
|
|
(see Figure 15-15.) its value is now the angle in the circle. Because the radius of the circle is so small (~10-33 cm), the value of the angle is completely unobservable. Consequently, the laws of physics should be invariant under shifts in the angle. This behaviour is reminiscent of the internal rotation mentioned earlier in the U(1) symmetry and they can be identified with each others. Therefore, distortion of this curled-up dimension corresponds to the presence of spin-1 gauge bosons. Actually the compactification is on a six-dimensional space, the theory of superstring severely restrict the geometrical form. It has been shown that a particular class of six-dimensional geometrical shapes called Calabi-Yau spaces can meet these conditions. Figure 15-16 shows the ordinary space (in two-dimension) with the curled-up Calabi-Yau space at each point. It is drawn only on the intersecting grid lines for visual clarity.
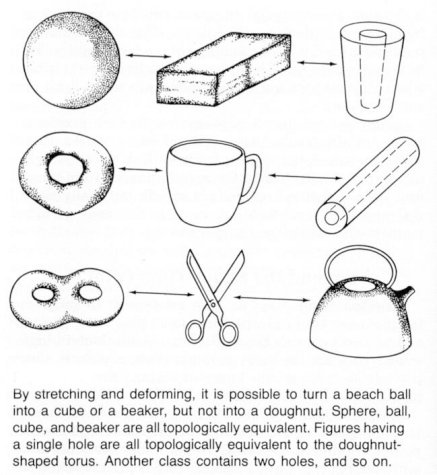 |
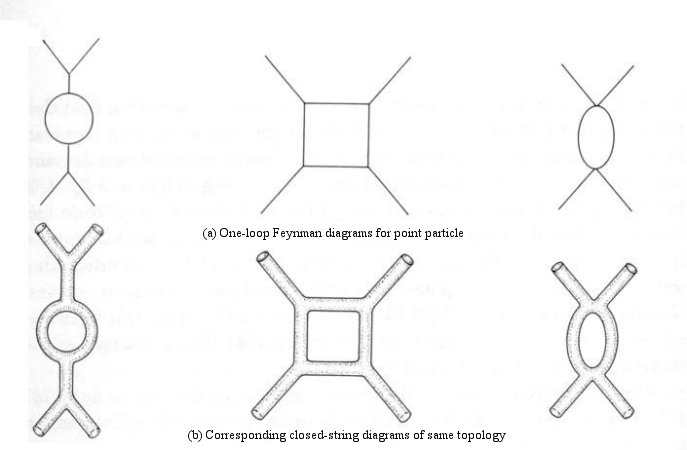 |
Topology becomes an important tool in superstring when it is treated as quantum mechanical object. This branch of mathematics is concerned with smooth, gradual, continuous change of geometric shape. For example, a square can be continuously deformed into a circle by pushing in the corners and rounding the sides. The essential rule is that no new hole can be created in the new form by tearing. Some topological equivalent objects are shown in Figure 15-17. Thus, as shown in Figure 15-18a, several one-loop Feynman
|
| |
Figure 15-18a Feynman Diagrams, Closed-string [view large image] |
diagrams for point particle can now be represented by just one closed-string diagram of the same topology.
|
 |
 |
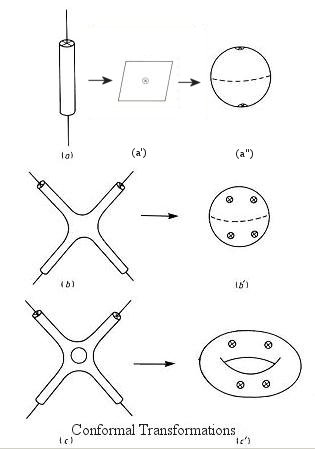
String theory is invariant under conformal transformations (Figure 15-18b). Such change in topology makes it feasible to evaluate string diagrams. Among other things this makes it possible to compactify the world sheet, closing off the holes corresponding to incoming and outgoing strings. For example, a world sheet with one incoming and one outgoing string (as in (a) of Figure 15-18b) can be conformally mapped to the plane of (a') with the incoming string appearing at the origin and the outgoing string at infinity (not shown) or to the sphere of (a") with the incoming and outgoing strings appearing at the south and north poles. The external string states in (b) of Figure 15-18b with four awkward legs are projected to points as indicated in (b').
|
| |
|
|
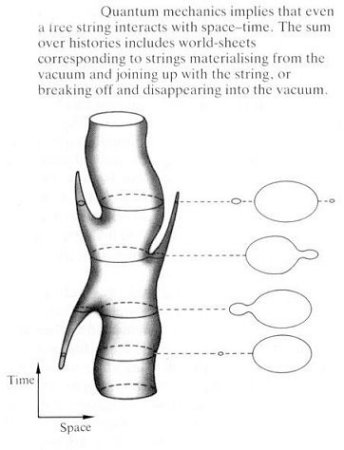
It has been mentioned in Topic-12 that the transition from classical to quantum field is via the sum over all possible paths in evaluating the Action. In superstrings, there are two parameters along the worldsheet (in the integral defining the Action) and the sum is over all possible connected surfaces. In particular, it includes all the surfaces formed by stretching, pulling, twisting and otherwise deforming (without tearing) the classical world-sheet. So included in the sum are surfaces with very long, thin tentacles as shown in Figure 15-18c. These tentacles can be interpreted as very small closed strings that appear from out the vacuum and join on the the original string, or as closed strings which break off from the original and then disappear into the vacuum.
 |
Interaction between two strings can be portrayed by a diagram similar to the Feynman diagram for the interaction of two point particles. In place of lines and points in the latter case, the paths of the strings become tubes. The two strings do not meet at a point, they interact by merging (from the incoming) and splitting (to the outgoing). Such a smearing of the interaction avoids the singularity at the point where the two particles meet and thus the theory of string is not plagued by the infinities in point particle
|
| |
|
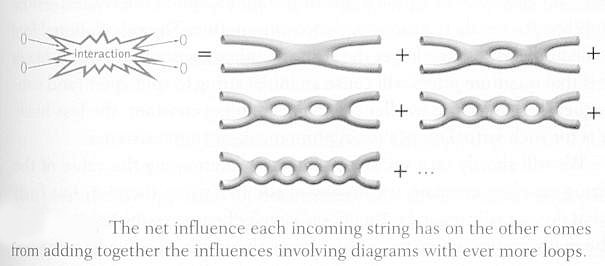
quantum field theories. Perturbation theory is used to expand the interaction into a sum of individual diagrams as shown in Figure 15-19. The first one is the main part called tree-level diagram. The others with increasing number of holes are called loop diagrams, they are contributions from virtual particle pairs. If the interaction strength is small, the series would converge rapidly, otherwise calculation becomes increasingly difficult as the number of loops grows.
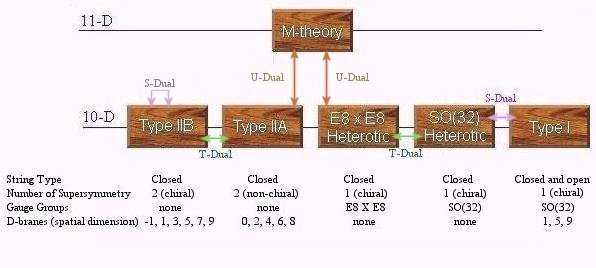 |
According to the differences in the number of supersymmetry, gauge groups, kinds of strings or branes, etc. there are five different versions of superstrings theories as shown in Figure 15-20. They are connected by the S-duality, which relates the strong coupling limit of one theory to the weak coupling limit of another theory; and the T-duality, which relates a theory which is compactified on a circle with radius R, to another theory compactified on a circle with radius 1/R. These 10-dimension theories are ultimately linked to the 11-dimension M theory.
|
| |
|
In 1995, Edward Witten gave evidence for a new, profound kind of duality. He suggested that the five theories, although apparently different in their basic construction, are all just different ways of describing the same underlying physics. The five theories are just five different windows onto this single theoretical framework (in 11-dimensions), which is now called the M-Theory. M-theory contains extended objects of a whole slew of different spatial dimensions called p-brane (an object with p space dimensions, up to nine). It seems the fundamental ingredients in the M-theory are "branes" of a variety of dimensions. The objects in the five theories show up only as strings (or membranes curled up to look like strings), which are light enough to make contact with physics as we know it. The perturbative analyses are not refined enough to discover even the existence of the super-massive extended objects of other dimensions; strings dominated the analyses and the theories was given the name of "string theories".
Currently there is no testable predictions from superstrings. However, it can be shown that at energies below 1016 Gev, the heterotic string theory effectively leads to an ordinary grand unified theory. Meanwhile at this moment, superstrings is the only viable theory that can unify the four interactions (See Figure 15-04), and have the potential to provide explanations for all the fundamental phenomena. It could take the place at the end of the long journey toward the ultimate theory as depicted in Figure 15-05a and 15-05b.
Further details on this subject can be found in the appendix - "Superstring Theory".
[Top]
Manifold, Vacuum Energy, and Multiverse
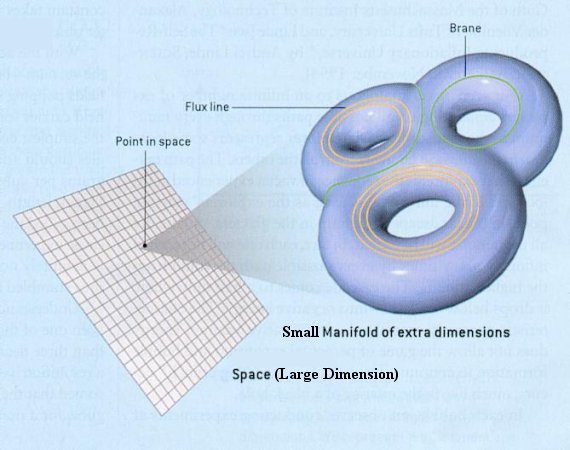 |
Research in the early 2000s indicates that the string theory may provide the explanations for "dark energy" and the origin of the "Big Bang". As mentioned earlier, the six extra dimensions curl up into tiny six-dimensional space known as manifold (see Figure 15-21). The equations of string theory specify the arrangement of the manifold configuration, along with their associated branes (green) and lines of force known as flux lines (orange). The physics that is observed in the three large dimensions depends on the size and the structure of the manifold: how many doughnut-like "handles" it has, the length and circumference of each handle, the number and locations of its branes, and the number of flux lines wrapped around each doughnut.
|
| |
|
Each manifold has an unique potential energy, contributed by fluxes, branes and the curvature of the curled-up dimensions. This energy is called the vacuum energy, because it is the energy of the spacetime when the large four dimensions are completely devoid of matter or fields. The geometry of the small manifold will try to adjust to minimize this energy. As the
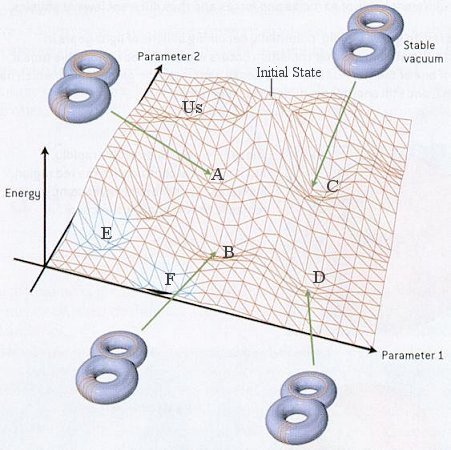 |
result, each stable configuration will settle down into the minimum of the vacuum energy as shown by the alphabets in Figure 15-22, where the negative energy is plotted in blue. The diagram depicts a simplified version of only two parameters. Actually, the number of adjustable parameters is enormous. There are solutions with up to about 500 handles and the number of flux lines can be as many as 10. Thus, the number of possible manifold configurations would be around 10500, and each would occupy a stable position in the energy map of multiple parameters. Our universe (see Us in diagram) happens to be one of these with a small cosmological constant (corresponding to the small but positive vacuum energy), which is now driving the observed cosmic acceleration. Large positive vacuum energy will produce too much acceleration, and negative vacuum energy will induce collapse. According to the anthropic principle, we are also living in such a manifold (of the six small dimensions) that the physical laws are suitable for the development of life.
|
| | |
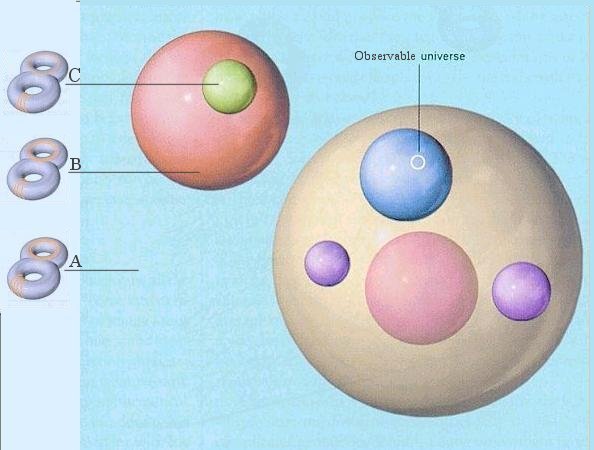 |
The possibility of decay from one stable vacuum to another suggests a radical new picture of the universe. Figure 15-23 depicts the large dimension space in color. The blue region represents an universe originally sitting in the minimum vacuum energy A (as shown in Figure 15-22). Decay of a flux line in A creates a different manifold, which tunnels to a new minimum in B (see Figure 15-22 and the red bubble in Figure 15-23). Then decay of another flux line in B creates another manifold, which tunnels to another new minimum in C (see Figure 15-22 and the green bubble in Figure 15-23), and so on ad infinitum. The whole universe is therefore a foam of expanding bubbles within bubbles, each with its own laws of physics. Extremely few of the bubbles are suitable
|
| | for the formation of complex structures such as galaxies and life. The observable universe is a relatively small region within one of these bubbles as shown in Figure 15-23. The Big Bang was just the beginning of a new manifold within an older universe. |
[Top]
By combining the laws of quantum mechanics and general relativity, it is deduced that in a region the size of the Planck length (10-33 cm.), the vacuum fluctuations are so huge that space as we know it "boils" and becomes a froth of quantum foam. In such a scenario, the space appears completely smooth at the scale of 10-12 cm.; a certain roughness starts to show up at the scale of 10-30 cm.; and at the scale of the Planck length space becomes a froth of probabilistic quantum foam (as shown in Figure 15-24) and the notion of a simple, continuous space becomes inconsistent. According to the latest idea in superstring theory, the space at such small scale cannot be described by the Cartesian coordinates, x, y and z; it should be replaced by
 |
"noncommutative geometry", where the coordinates are represented by non-diagonal matrix. In other word, it is impossible to determine the coordinates precisely at any one time. This is essentially the extension of the uncertainty principle in quantum mechanics. Thus, at the small scale, the usual notion of space has broken down. However, it is found that large pieces of relativity theory, quantum theoyr and particle physics can be carried over into such a world. In the last few years theoretical physicists have been surprised to discover that both loop quantum gravity and superstring theory describe worlds in which the geometry is noncommutative, which can be used now as a new language to compare the two theories.
|
|
|
A theory to describe space with the size of the Planck length has been developed sicne the 1950s. It is called theory of loop quantum gravity, which postulates that the minimum linear size of space is of the order of the Planck length. Space with larger expanse are built upon this lowest size such that the area and volume are quantized as shown in Figure 15-25. In the loop
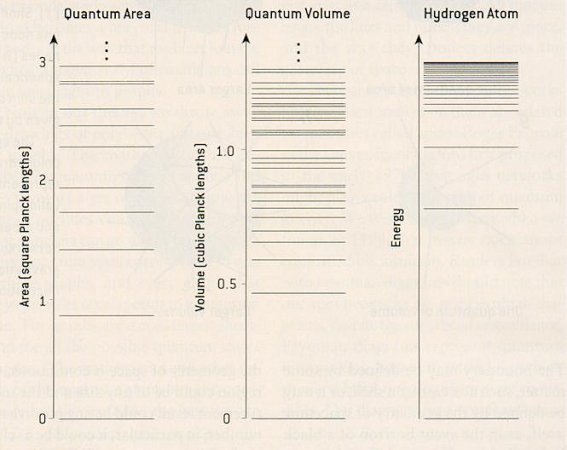 |
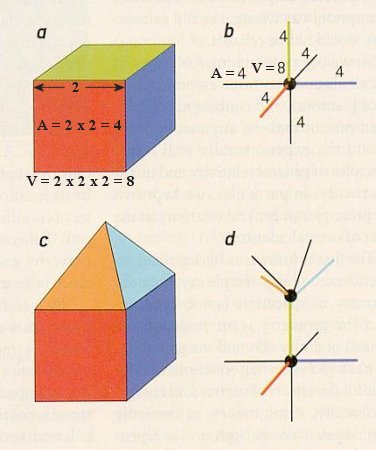 |
quantum gravity formulation, the length is not the fundamental attribute. The theory is based on quantized angular momentum, which corresponds to an oriented area element. Thus the area is more fundamental than the length. There is a nonzero absolution minimum volume about 10-99 cm3, and it restricts the set of larger volumes to a discrete series of numbers. These quantum states are similar to the energy levels of the hydrogen atom. The idea is similar to the macroscopic and microscopic views of matter, for which the continuous apperance gradually changed to an assembly of discrete atoms at small scale.
|
|
|
|
Description of a quantum of space can be simplified by representing the volume with a dot or node, and the area (enclosing the volume) with a line perpendicular to the face (see Figure 15-26 a and b). The numbers for the node or line (in Figure 15-26 b) indicate the size of the volume or area. In this case, the quantum of the volume has eight units of the cubic Planck length. Figure 15-26 c and d show the connection of two volumes and its representation in nodes and lines. The network in Figure 15-27 shows the connection of many discrete volumes; it is called the "spin network". Particles, such as electrons, correspond to certain types of nodes, which are represented by adding more labels on the nodes. Field, such as the electromagnetic field, are represented by additional labels on the lines of the graph.
Just as space is defined by a spin network's discrete geometry, time is defined by the sequence of distinct moves that rearrange the network, as shown in Figure 15-27. Time flows not like a river but like the ticking of a clock, with "ticks" that are about as long as the Planck time: 10-43 second. Or, more precisely, time in the universe flows by the ticking of innumerable clocks -
 |
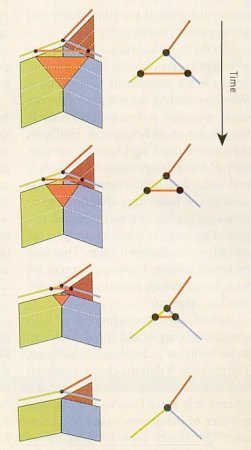 |
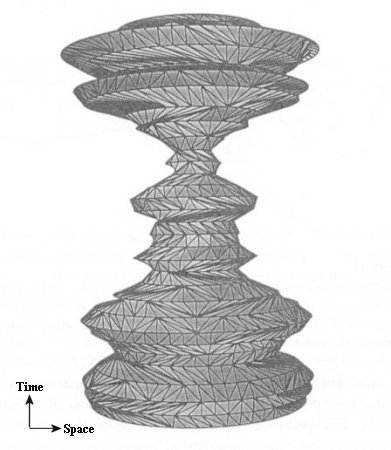
in a sense, at every location in the spin network where a quantum "move" takes place, a clock at that location has ticked once. In Figure 15-28, the lines of the spin network become planes, and the nodes become lines. The result is called a spin foam. Taking a slice through a spin foam at a particular time yields a spin network; taking a series of slices at different times (jumping from one dotted line to another) produces frames of a movie showing the spin network evolving in time. The sequence on the right-hand side of Figure 15-28 shows a connected group of three volume quanta merge to become a single one. Figure 15-27 is a computer model of a quantum spacetime, showing the evolution of the spin network. It portrays the strong fluctuation caused by the uncertainty principle.
|
|
|
|
Predictions and Tests:
- An important test is whether classical general relativity can be recovered as an approximation to the loop quantum gravity. It has been shown that long-wavelength gravitational waves propagating on otherwise flat space can be described as excitations of specific quantum states in the loop quantum gravity theory. The theory can also reproduce blackhole radiation and the relationship between blackhole's entropy and its surface area.
- The Planck scale is 16 orders of magnitude below the scale probed in the highest-energy particle accelerators currently planned (higher energy is needed to probe shorter distance scales). Thus there seems to be hopeless for the confirmation of quantum gravity theories.
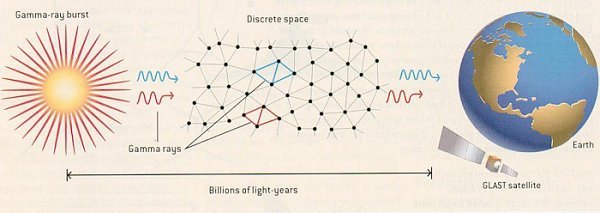 |
Nevertheless, radiation from distant cosmic explosions called gamma-ray bursts might provide a way to test whether the theory of loop quantum gravity is correct. Gamma-ray bursts occur billions of light-years away and emit a huge amount of gamma rays within a short span. According to loop quantum gravity, each photon occupies a region of lines at each instant as it moves
|
|
through the spin network. The discrete nature of space causes higher-energy gamma rays to travel slightly faster than lower- |
energy ones. The difference is tiny, but its effect steadily accumulating during the rays' billion-year voyage. If a burst's gamma rays arrive at Earth in slightly different times according to their energy, that would be evidence for loop quantum gravity (see Figure 15-29). The GLAST satellite, which is scheduled to be launched in 2005, will have the required sensitivity for this experiment.
- Another possible effect of discrete spacetime involves very high energy cosmic rays. It was predicted that cosmic-ray protons with an energy greater than 3x1019 ev would scatter off the cosmic microwave background that fills space and should there fore never reach the Earth. However, more than 10 cosmic rays with energy over this limit were detected in an experiment called AGASA. It turns out that the discrete structure of space can raise the energy required for the scattering reaction, allowing higher-energy cosmic-ray protons to reach the Earth. If the ASASA observations hold up, and if no other explanation is found, then it may turn out that the discreteness of space has already been detected.
- Loop quantum gravity has opened up a new window to investigate deep cosmological questions such as the origin of the universe. Recent loop quantum gravity calculations indicate that the big bang is actually a big bounce; before the bounce the universe was rapidly contracting. A question of similar profundity concerns the cosmological constant. Recent observations of distant supernovae and the cosmic microwave background strongly indicate that it is associated with a positive energy, which accelerates the universe's expansion. Loop quantum gravity has no trouble incorporating this fact into the theory.
- It remains to be shown that classical general relativity is a good approximate description of the loop quantum gravity theory for distances much larger than the Planck length, in all circumstances; and whether special relativity must be modified at extremely high energies (loop quantum gravity indicates that the universal speed of light is only valid for low energy photons).
- Unlike the superstring theory, loop quantum gravity is completely unperturbative and is also background-independent (geometry of spacetime is not fixed), and appears to lead to a pregeometry in which space and time are derived concepts (instead of being a pre-defined entity).
- There is no link between the loop quantum theory and the superstring theory. While the supporters of the former stress the shortcoming of relying on a pre-defined space-time frame (in the superstring theory), and thus will not provide an adequate description of gravitation at small scale; the supporters of the superstring theory point out that the interaction between gravitons and other particles is inconsistent in loop quantum theory. It is suggested that both camps perceive only a small aspect of the whole thing - like the blind men and the elephant. It is siggested that string theory and loop quantum gravity are each part of a single theory. Each is correct, in the sense that it describes to a good approximation in a certain limited domain. The string theory is able to provide a framework for the graviton as mode of excitation of a string, while the loop quantum theory prescribes a way to make a background independent theory. Thus, each solves part of the problem. But each also has limits which prevent it from forming the basis for a complete theory of nature. It is regrettable that physicists work exclusively only in one group or the other.
[Top]
1Inertial systems of reference are either at rest or moving with constant velocity relative to each other.
2In general, the function of a field F is complex, which can be decomposed into the form: F = FR + iFI similar to the complex number c = a + ib. The real part FR and the imaginary part FI correspond to particle with negative and positive charge respectively.
3It is found that only fermions with left-handed chirality participates in weak interaction. The chirality in elementary particle is related to the property of spin. A right-handed particle has its spin oriented along the particle's direction of motion, while the spin of a left-handed particle points the other way. All neutrinos are left-handed, and all antineutrinos are right-handed (if the neutrino mass is strictly zero). Other particles can exist in either state.
4In the summer of 1953 C. N. Yang and Robert Mills (a graduate student at that time) invented the SU(2) gauge theory that has become synonymous with their names. They did not immediately publish their results because they were aware of the difficult problems posed by the gauge-field masses and renormalization. After studying these problems for some time and realizing that they would not be solved in the short term, they sent their paper for publication in the spring of 1954. The problems were eventually resolved twenty years later in a modern version called the Standard Model.
5The transition is similar to water frozen to ice, the Higgs fields move away from a state with higher symmetry to a state without this symmetry but in lower energy. This is called spontaneous symmetry breaking. It is related to the fact that although the system has certain symmetry as portrayed in the "Action", the field itself needs not to possess the same kind of symmetry. According to GUT (Grand Unified Theory), the transition occurred at about 10-37 sec after the Big Bang when temperature was 1029 oK corresponding to 1016 Gev.
[Top]
[Top]
Abelian group
Accelerators
Asymptotic freedom
Bare mass
Baryon
Beta decay
Bubble chamber
Calabi-Yau space
CERN, LHC
Charge Carriers
Cloud chamber
Collider
Colour charge
Compactification
Cosmic rays
Cyclotron
Einstein, Albert
Electroweak interaction
Elementary particles
Fermi, Enrico
Fermilab Tevatron
Fermion generations
Feynman diagram
Field equation
Fundamental interactions
Gauge boson
Gauge invariance
General theory of relativity
Geodesic
Ghosts
Gluon
Grand Unified Theory (GUT)
Graviton
Gravity
Green's function
Hardon
Heterotic superstring
Hierarchy problem
Higgs field
Higgs mechanism
Lee, T. D. and Yang, C. N.
Loop quantum gravity
Manifold
Manyfold universe
Maxwell, J. C.
| |
Meson
M-theory
Newton, Isaac
Neutrino
Non-Abelian group
Parity violation
P-brane
Perturbation method
Quantum Chromodynamics (QCD)
Quantum domain
Quantum electrodynamics (QED)
Quantum field theory
Quark
Quark confinement
Renormalization
S-duality
Second quantization
Sheldon Glashow, Abdus Salam, Steven Weinberg
S matrix
Special theory of relativity
Spontaneous symmetry breaking
Standard model
Strong residual interaction
SU(2)
SU(3)
SU(5)
Super-gravity
Superpartners
Superstrings
Supersymmetry
Synchrotron
Tachyon
T-duality
Theory Of Everything (TOE)
Topology
Top quark events
U(1)
Unifications, A Brief History of Physcis
Van de Graaff generator
Colour charge
W bosons
World-sheet
X bosons
Yukawa, H.
|















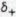 factors in the mathematical expression represent the probobility amplitude of the process between points (s56 is the distance travels by the photon). At the vertex (intersection), the likelihood that an electron would emit or absorb a photon is e
factors in the mathematical expression represent the probobility amplitude of the process between points (s56 is the distance travels by the photon). At the vertex (intersection), the likelihood that an electron would emit or absorb a photon is e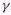
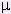 , where e is the electron's charge and
, where e is the electron's charge and 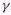
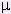 a vector called Dirac matrices to keep track of the electron's spin. Conversely, a process can be computed by drawing graphs and then applying the Feynman rules. The trouble with Feynman's method is that it always leads to infinite expressions for the loop diagrams such as those in the fourth order electron-electron scattering (diagrams a - i in Figure 15-05k). However, Feynman and others discovered that these are related only
a vector called Dirac matrices to keep track of the electron's spin. Conversely, a process can be computed by drawing graphs and then applying the Feynman rules. The trouble with Feynman's method is that it always leads to infinite expressions for the loop diagrams such as those in the fourth order electron-electron scattering (diagrams a - i in Figure 15-05k). However, Feynman and others discovered that these are related only 
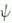 (x,t) =
(x,t) = 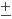
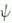 (-x,t). The overall parity is given by the multiplication of its parts, e.g. (+1)x(-1)x(+1) = (-1) etc. It has been long held that parity is conserved before and after all particle interactions. The processes in which parity is not conserved would look different in the mirror image (+ 180o rotation) world. With some hints from experimental
(-x,t). The overall parity is given by the multiplication of its parts, e.g. (+1)x(-1)x(+1) = (-1) etc. It has been long held that parity is conserved before and after all particle interactions. The processes in which parity is not conserved would look different in the mirror image (+ 180o rotation) world. With some hints from experimental 




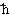 is for quantum, and the velocity of light c comes with special relativity. In quantum gravity, all the fundamental units are expressed in terms of G,
is for quantum, and the velocity of light c comes with special relativity. In quantum gravity, all the fundamental units are expressed in terms of G, 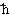 , and c: Planck length = (G
, and c: Planck length = (G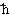 /c3)1/2 = 1.62x10-33 cm, Planck time = (G
/c3)1/2 = 1.62x10-33 cm, Planck time = (G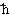 /c5)1/2 = 5.39x10-44 sec, Planck mass = (
/c5)1/2 = 5.39x10-44 sec, Planck mass = (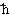 c/G)1/2 = 2.17x10-5 gm, Planck energy = (
c/G)1/2 = 2.17x10-5 gm, Planck energy = (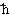 c5/G)1/2 = 1.22x1019 Gev, and Planck temperature = (
c5/G)1/2 = 1.22x1019 Gev, and Planck temperature = (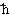 c5/GkB2)1/2 = 1.42x1032 oK, where kB is the Boltzmann's constant, which relates energy to absolute temperature on the Kelvin scale.
c5/GkB2)1/2 = 1.42x1032 oK, where kB is the Boltzmann's constant, which relates energy to absolute temperature on the Kelvin scale.
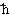 . The Schrodinger equation was developed and applied to the atomic and molecular system with great success. This formalism becomes increasingly inaccurate for phenomena in smaller domain where energy can manifest itself in a variety of ways, e.g., pair creation or particle moving at relativistic speed. Therefore, the Schrodinger equation has to be replaced by field equations such as the Klein-Gordon equation (for particle with no spin) or Dirac equation (for particle with spin 1/2). These field equations are invariant (unchanged) under a change of the space-time coordinate system (Lorentz transformation). It is referred to as relativistic invariance, which ensures the validity of the field equation at relativistic speed. To account for the creation/annihilation of particles in high energy interaction, the field is considered to be an operator. It is expanded into Fourier series in terms of harmonic functions and coefficients. These coefficients are then subjected to some quantization rules. Depending on whether the particle has integer or half integer spin, these operators satisfy the commutation or anti-commutation relations (for example: ab + ba = 1; the Pauli exclusion principle is guaranteed by quantization with the anti-commutation relations for spin 1/2 particles). They are the creation and annihilation operators, which operate on state vectors describing the number of particles in different states. This is called the second quantization, which endows particle property to the field (field + second quantization = quantum field). Thus, in quantum field theory the particles are just bundles of energy and momentum of the fields, which constitute the basic ingredient. A more mathematically oriented description on Quantum Field Theory can be found in the appendix.
. The Schrodinger equation was developed and applied to the atomic and molecular system with great success. This formalism becomes increasingly inaccurate for phenomena in smaller domain where energy can manifest itself in a variety of ways, e.g., pair creation or particle moving at relativistic speed. Therefore, the Schrodinger equation has to be replaced by field equations such as the Klein-Gordon equation (for particle with no spin) or Dirac equation (for particle with spin 1/2). These field equations are invariant (unchanged) under a change of the space-time coordinate system (Lorentz transformation). It is referred to as relativistic invariance, which ensures the validity of the field equation at relativistic speed. To account for the creation/annihilation of particles in high energy interaction, the field is considered to be an operator. It is expanded into Fourier series in terms of harmonic functions and coefficients. These coefficients are then subjected to some quantization rules. Depending on whether the particle has integer or half integer spin, these operators satisfy the commutation or anti-commutation relations (for example: ab + ba = 1; the Pauli exclusion principle is guaranteed by quantization with the anti-commutation relations for spin 1/2 particles). They are the creation and annihilation operators, which operate on state vectors describing the number of particles in different states. This is called the second quantization, which endows particle property to the field (field + second quantization = quantum field). Thus, in quantum field theory the particles are just bundles of energy and momentum of the fields, which constitute the basic ingredient. A more mathematically oriented description on Quantum Field Theory can be found in the appendix.


























