dU = dQ + dW ---------- (1)
where dQ and dW are positive for energy transfer from the surroundings to the system, and negative for energy transfer from the system to the surroundings. If the process of energy transfer is broken down into finer details, e.g., change in disorder (dS), volume expansion/contraction (dV), and adding a new species of particles (dN), then the change in internal energy can be expressed as:
dU = T dS - p dV +
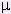 dN ---------- (2)
dN ---------- (2)U= (3nR/2) T ---------- (3)
where R = 8.314x107 erg/Ko-mole is called the gas constant.
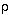 ) is defined as mass per unit volume.
) is defined as mass per unit volume.dS = dQ / T or dQ = T dS ---------- (4)
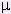 ) of a thermodynamic system is the change in the energy of the system when a different kind of constituent particle is introduced, with the entropy and volume held fixed.
) of a thermodynamic system is the change in the energy of the system when a different kind of constituent particle is introduced, with the entropy and volume held fixed. 
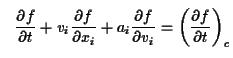
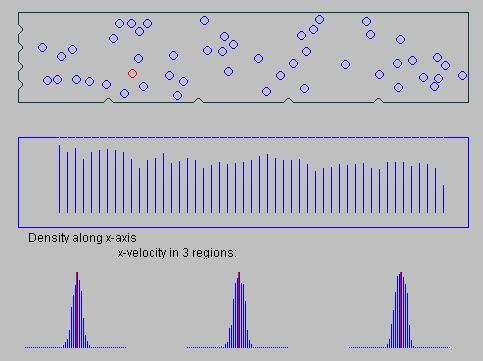
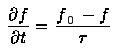
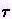 is the relaxation time - a characteristic decay constant for returning to the equilibrium state, and f0 is the equilibrium distribution. The solution for this equation is:
is the relaxation time - a characteristic decay constant for returning to the equilibrium state, and f0 is the equilibrium distribution. The solution for this equation is: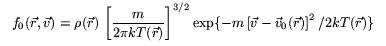
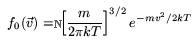
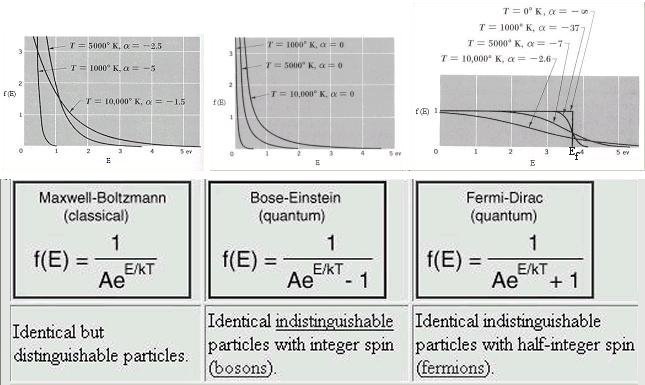
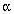 is a normalization constant. The classical and Bose-Einstein distribution are similar except when kT >> E. Near absolute zero
is a normalization constant. The classical and Bose-Einstein distribution are similar except when kT >> E. Near absolute zero