
| Home Page | Overview | Site Map | Index | Appendix | Illustration | FAQ | About | Contact |
 |
 |
The Periodic Table in Figure 13-01a is the modern version; while Figure 12-19 depicts the simpler one. The atomic number is the number of positive charges in the atomic nucleus. Atomic masses refer to the masses of neutral atoms, including the masses of the electrons and the mass equivalent of their binding energies. It is expressed in mass units such that the mass of the most abundant type of carbon is exactly |
Figure 13-01a Periodic Table, |
Figure 13-01b Periodic Table, |
12.00 u (1 u = 1.66x10-24 gm). |
 |
the boiling point, melting point, density, acidity, basicity, crystal structure, and electronegativity (tendency to keep electrons) of the elements. The s, p, d, and f letters in the electronic configuration designate the orbital quantum number l = 0, 1, 2, 3, ... respectively for the outer shell electrons. A new designation of the groups has a number ranged from 1 to 18. Figure 13-01b is an unconventional Periodic Table. It specifies the phase (solid, liquid, or gas) of the element at room temperature, whether the element is radioactive or man-made, as well as its usage (in daily life) or occurrence (in nature). Only a few of the elements are edible as shown in Figure 13-01c. Other kinds of Periodic Table may incorporate properties such as atomic radius, covalent radius, ionization potential, specific heat, heat of vaporization, heat of fusion, electrical conductivity, and thermal conductivity etc. |
Figure 13-01c Periodic Table, Comical [view large image] |
The regular pattern in the periodic table is related to the state of the electron in an atom. It is specified by four quantum numbers. The principal quantum number n determines the energy level; its value runs from 1, 2, 3, ... For each n, the orbital quantum number l = 0, 1, 2, ... (n-1); it is related to the magnitude of angular momentum. Then for each l, the magnetic quantum number m can be -l, -l+1, ...l-1, l; it is related to the z component of the angular momentum. The spin quantum number s is either +1/2 or -1/2. For n = 1, l = 0, m = 0, there is only 2 possible quantum states for the electron, with s = +1/2 and -1/2 respectively. For n = 2, l = 0, m = 0 and l =1, m = -1, 0, +1; there is a total of 2 + 6 = 8 possible quantum states. Therefore, it requires 2 electrons to complete the shell for n = 1, and 8 electrons to complete the shell for n = 2, ...and so on. The orbital quantum number l is often designated by a letter, s for l = 0, p for l = 1, d for l = 2, and f for l = 3 ... The quantum number l is non-additive while m is additive and relates to an Abelian group (e.g., the two dimensional rotation about the z-axis). Particles having the same non-additive quantum numbers but differing from each other by their additive quantum numbers are said to belong to the same multiplet. The number of members of a multiplet is called its multiplicity. For a given multiplet l the multiplictiy is equal to 2l+1. The atom tends to lost the outer electrons if the number is far from a complete shell or sub-shell such as the elements in the beginning of a series. It gradually develops a preference for accepting more electrons to complete the outer shell as the progression moves toward the end of a series. This property is responsible for all the chemical reactions. A stable atomic configuration is achieved by completing a shell or sub-shell as illustrated in Table 13-01 below by the inert elements (the rule becomes more complicated in the advanced series as the electrons with high l tend to intermingle with each others), which do not react chemically:
| n | l | (2l+1)x2 | Electron Configuration of the Inert Element |
|---|---|---|---|
| 1 | 0 | 2 | 2He (2)=2 |
| 2 | 0, 1 | 2, 6 | 10Ne (2)+(2+6)=10 |
| 3 | 0, 1, 2 | 2, 6, 10 | 18Ar (2)+(2+6)+(2+6)=18 |
| 4 | 0, 1, 2, 3 | 2, 6, 10, 14 | 36Kr (2)+(2+6)+(2+6+10)+(2+6)=36 |
| 5 | 0, 1, 2, 3, 4 | 2, 6, 10, 14, 18 | 54Xe (2)+(2+6)+(2+6+10)+(2+6+10)+(2+6)=54 |
| 6 | 0, 1, 2, 3, 4, 5 | 2, 6, 10, 14, 18, 22 | 86Rn (2)+(2+6)+(2+6+10)+(2+6+10+14)+(2+6+10)+(2+6)=86 |
 |
creator in Greek), with a solitary electron, nominally belongs in the alkali metals group. However, removal of that single electron requires considerably more energy than for the other alkali metals. Like the halogens, only one additional electron is required to fill in the outermost shell of the hydrogen atom, so hydrogen can be regarded in some respects as behaving like a halogen; its elemental form is a diatomic gas, and it can even form salts (called hydrides) with the alkali metals, where the metal has donated an electron to the hydrogen, almost as if hydrogen were actually a halogen. |
Figure 13-02a Lithium |
 |
|
Figure 13-02b Beryl |
 |
|
Figure 13-02c Gold |
reflecting element. Silver also has the unusual property that the tarnish that forms on silver is still highly electrically conductive. |
 |
abundant element in the earth's crust. Aluminum is found as aluminum oxide in the ore called bauxite. Aluminum is extremely valuable in industry (see Figure 13-02d). It is light, strong, and does not tarnish in air. It is a good conductor and is used in wiring, airplane parts, household items. The other members of the boron family ...gallium, indium, and thallium, are metals. Gallium shares many chemical properties with aluminum. It is an extremely soft metal that can be cut with a knife. It also has an extremely low melting point of 29.8oC. Gallium arsenide (GaAs) can function as a "laser diode" and convert electricity directly into a beam of laser light. |
Figure 13-02d Aluminum |
 |
 |
mixing silica (sand - SiO2), soda ash (sodium carbonate - Na2CO3) and limestone (calcium carbonate - CaCO3) in a ratio of 60:80:5 and heated to the melting point of 2500oF. The final product is a supercooled liquid called glass which can be made to be colourful or to have special property by adding impurities (see Figure 13-02e2). Silicon is also used in solar cells, which convert the energy of sunlight into electric energy. Germanium is a metalloid used in transistors, which are devices found in many electronic instruments, such as radios and |
Figure 13-02e1 Carbon |
Figure 13-02e2 Glass |
televisions. Tin is a metal which resists rusting and corrosion. The most dense element in the carbon family is the metal lead (Pb), which can form poisonous compounds. |
 |
the military to make incendiary bomb. Arsenic is a brittle, crystalline solid at room temperature. It is often thought of as a semi-metal, or metalloid. For example, it is a poor conductor of electricity, yet it has a steel-gray color. In the form of arsenious oxide, it is a well-known poison. It is used as a weed killer and insecticide. Arsenic has become a material of great importance in the world of solid-state electronics. Small amounts of arsenic are added to such semi-conductors as germanium and silicon to transform them into transistors. |
Figure 13-02f Phosphorus |
 |
name is generally considered to mean "ore former" (from the Greek chalcos "ore" and -gen "formation"). Oxygen and sulfur (see Figure 13-02g) are nonmetals, polonium is a true metal, and selenium and tellurium are metalloid semiconductors (i.e., their electrical properties are between those of a metal and an insulator). Nevertheless, tellurium, as well as selenium, is often referred to as a metal when in elemental form. Chalcogenides are quite common as minerals, e.g., FeS2 pyrite is an iron ore and AuTe2 gave its name to the gold rush town of Telluride, Colorado in the USA. The oxidation number of the chalcogen is generally -2 in a chalcogenide but other values (e.g. -1 in pyrite) can be attained. The highest oxidation number +6 is found in sulfates, selenates and tellurates, e.g., in Na2SeO4 - sodium selenate. |
Figure 13-02g Sulfur |
 |
most carbon-containing, or organohalogen, molecules. Organohalogen chemicals (such as DDT, PCB, CFC, ...) are often believed to be solely industrial compounds, but many living organisms and geological phenomena also produce them naturally. In the case of plants and animals (such as sponges, corals, seaweeds, evergreen trees, some arthropods, and some frogs), the substance is produced for defence against predators and parasites. The halogens become less reactive, and their melting points increase further down the group. For example, fluorine is a yellow gas at room temperature, whereas bromine is a liquid, and iodine is a black solid (see Figure 13-02h). |
Figure 13- | 02h Iodine |
 |
 |
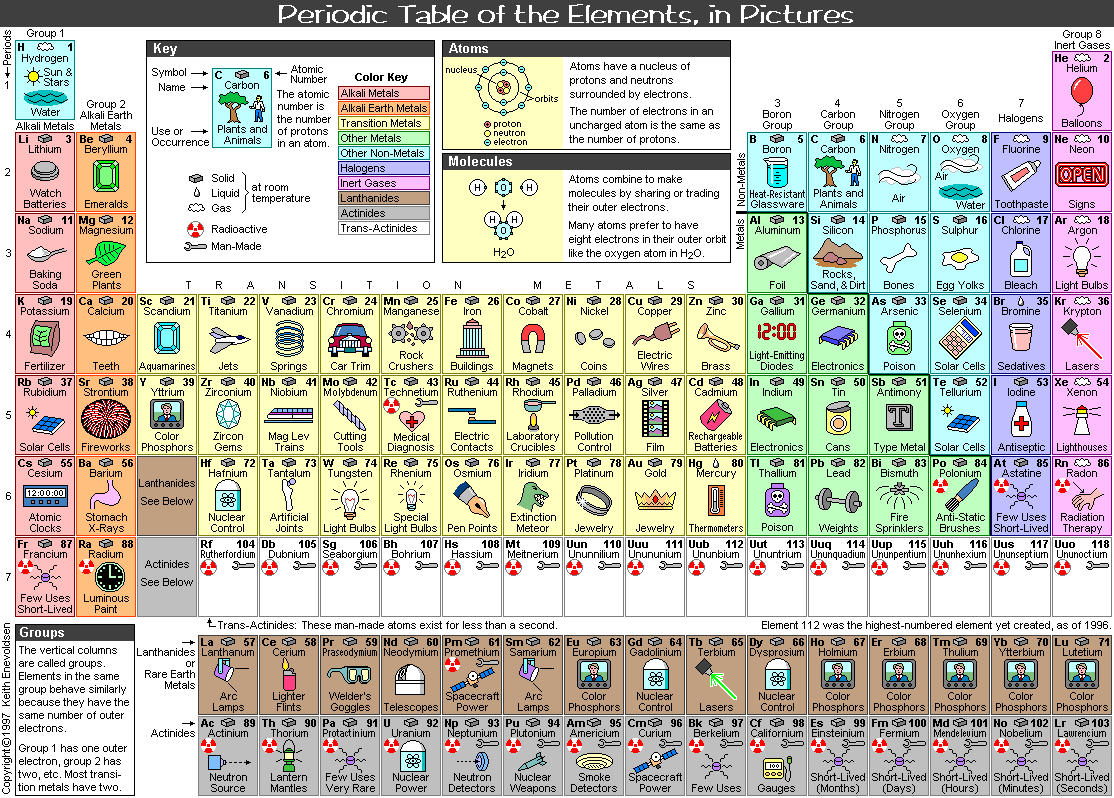
About 80% of the free elements at room temperature exists in the form of metal. The conditions to form metal are vacant valence orbitals and low ionization energies. Similar to the splitting of energy levels when two or more atoms come close to each other; (See Figure 12-15.) energy levels broadened to a band (many closely spaced energy levels) |
Figure 13-03 Energy Bands |
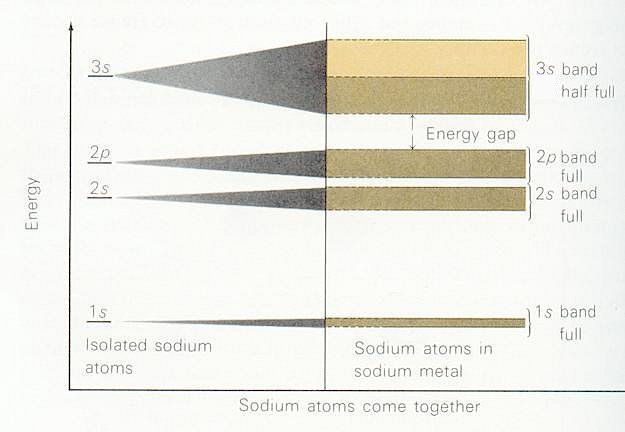
Figure 13-04 Band Theory |
for an aggregate of many atoms as shown in |
| Figure 13-03. In this example, the valence electrons occupy the energy bands up to half of the 3s band at 0oK, at an energy called Fermi energy Ef. Figure 13-04 shows that if there is empty levels available in the energy band, valence electrons will be able to roam among the space in between the atoms by absorbing energy from the environment when the temperature is above 0oK. With a few exceptions, metals have a silvery-white color because they reflect all frequencies of light. They have high electrical and thermal conductivity and all metals can be drawn into wires or hammered into sheets without shattering -- that is, they are ductile and malleable. All these attributes are the result of mobile, non-rigid electron gas within the lattice. Most metals (except gold, silver, platinum, and diamond) do not occur as free elements in the Earth's crust. They are usually | found in chemical combination with other elements as mineral ores.
Figure 13-04 shows that in an insulator, the valence band is full and the next empty energy band is separated by a large energy gap. Conduction cannot occur unless some of the electrons in the valence band are promoted to the conduction band. Energy needed to promote a few electrons might be provided by heating the solid to a very high temperature or by shining X rays on it. No solid can remain as a good insulator while it is exposed to X rays. A semiconductor has a small energy gap. Electrons can be promoted to the conduction band as a result of irradiation such as the conversion of sunlight to electricity by means of a silicon cell. |
 |
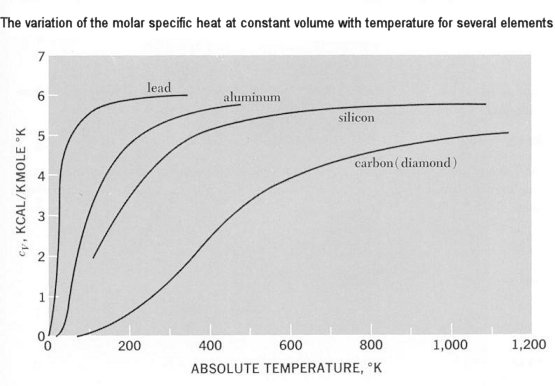 |
These waves, like electromagnetic waves in a cavity, have quantized energy contents. A quantum of vibrational energy in a solid is called a "phonon", and it travels with the speed of sound. The concept of phonones is quite general and has applications in connection with the thermal conductivity of some solids, and the way electrons in the crystal structure interact with sound waves. |
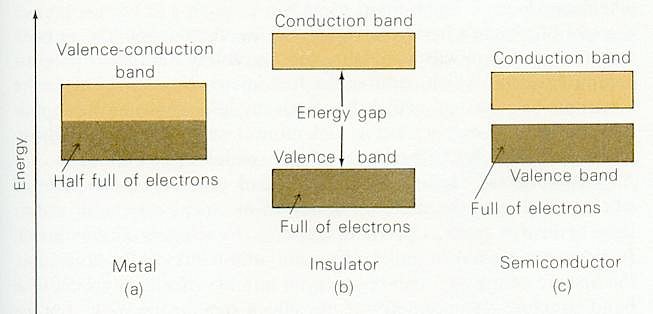
Figure 13-05 Crystal Types [view large image] |
Figure 13-06 Specific Heats |
 |
If mercury is cooled below 4.1 K, it loses all electric resistance. This discovery of superconductivity by H. Kammerlingh Onnes in 1911 was followed by the observation of other metals and intermetallic compounds (made of two or more metallic elements) which exhibit zero resistivity below a certain critical temperature Tc. The fact that the resistance is zero has been demonstrated by sustaining currents in superconducting lead rings for many years with no measurable reduction. Table 13-02 shows the elements, which can become superconducting at the indicated critical temperature.
[view large image] |
Table 13-02 Super-conducting Elements |
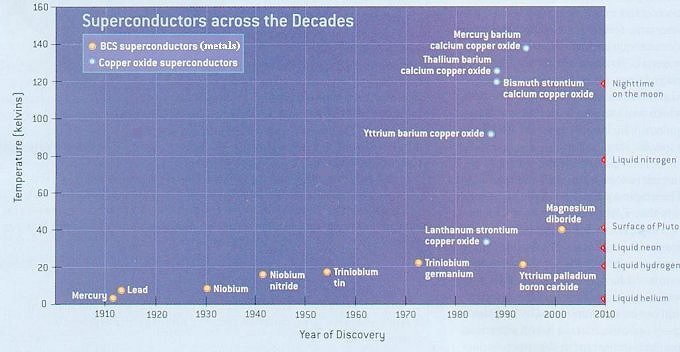 |
Ceramic materials are expected to be insulators -- certainly not superconductors, but that is just what Georg Bednorz and Alex Muller found when they studied the conductivity of a lanthanum-strontium-copper oxide ceramic in 1986. Its critical temperature of 30 K was the highest, which had been measured to date. Their discovery started a surge of activity which discovered superconducting behavior as high as 125 K. However, these compounds are hard to make and difficult to shape. They pose a multitude of physical challenges to researchers and engineers. |
Figure 13-07 High Temperature Superconductors [view large image] |
Figure 13-07 lists the high temperature (above 4o K) superconductors discovered during the last one hundred years. |
 |
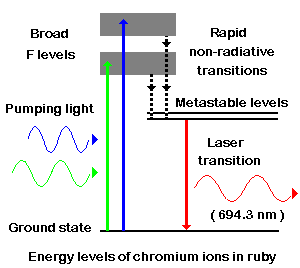 |
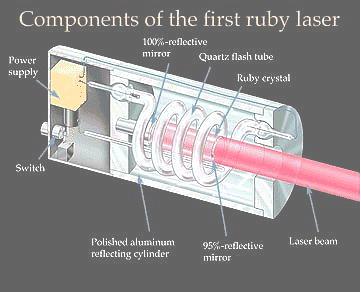
Finding substances in which a population inversion can be set up is central to the development of new kinds of laser. The first material used was synthetic ruby. Ruby is crystalline aluminum (Al2O3) in which a small fraction of the Al3+ ions have been replaced by chromium ions, Cr3+. It is the chromium ions that give rise to the characteristic pink or red colour of ruby and it is in these ions that a population inversion is set up in a ruby laser. |
Figure 13-09 Ruby Laser |
Figure 13-10 Laser, Energy |
 |
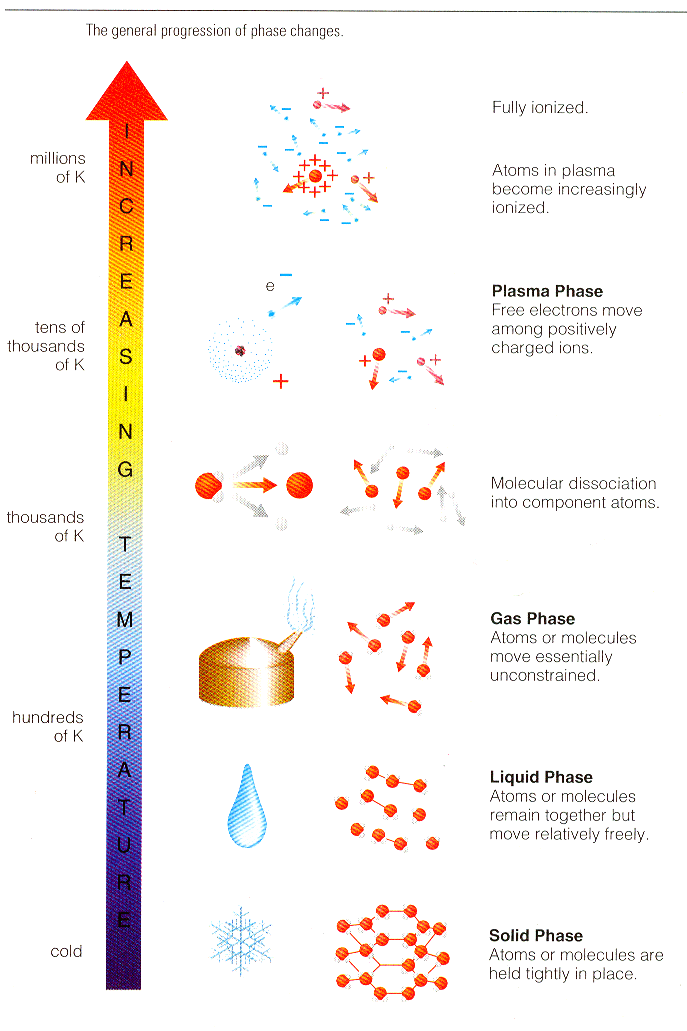 |
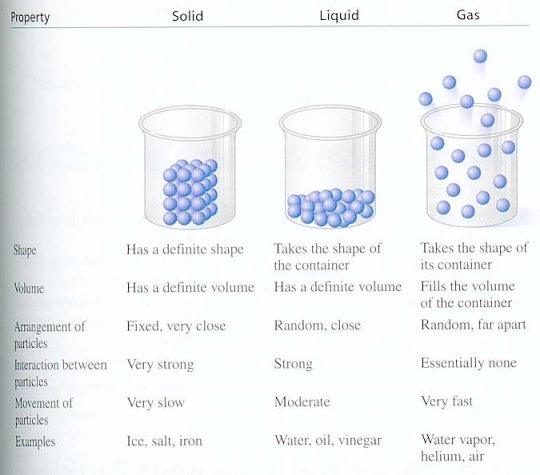
In the solid state, the atoms are firmly imprisoned inside a rigid network (like ice for example). When we raise the temperature, they go into a liquid state (the ice melts), where the atoms may slide around in relation to the others, thus enabling a liquid to adapt to the shape of a container. If we heat it up even more, we arrive at the gas state: atoms then move around freely and independently of each other (water turns into steam). (See Figure 13-11.) Finally, when we get to very high temperatures (typically several million degrees), the ingredients of the atom separate, nuclei and electrons move around independently and form a globally neutral mixture: this is the plasma state (See Figure 13-12). |
Figure 13-11 The Three Phases |
Figure 13-12 The Fourth |
|
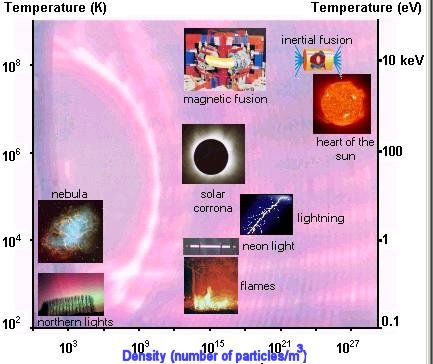
This fourth state of matter, found in the stars and the interstellar environment, makes up most of our universe (around 99 %). On Earth, it does not exist in a natural form, apart in lightning and the Aurora Borealis. In our everyday life, plasmas have many applications (micro-electronics, television flat screens and so on), of which the commonest is the neon tube. (See Figure 13-13.)
Depending on the temperature, the atoms may be partially or wholly ionized. A plasma may thus be considered as a mixture of positively charged ions and negatively charged | electrons, possibly co-existing with neutral atoms and molecules. For example, in our luminescent tube, the ions and electrons is a small proportion in relation to atoms and molecules. On the other hand, in plasmas produced for fusion experiments, the gas is strongly ionised, and the atoms and molecules are in low proportion, even completely absent in the heart of the pulse. In both cases, the description of plasmas comes from the physics of fluid mechanics and controlled by the force of electromagnetic interaction. The system is described by the usual macroscopic features such as density, temperature, pressure and rate of flow. |
 |
 |
The vast power radiated by the Sun is generated by the fusion process wherein light atoms combine with an accompanying release of energy. In nature, proper conditions for fusion occur only in the interior of stars. Researchers are attempting to produce the conditions that will permit fusion to take place on earth.
Since nuclei carry positive charges, they normally repel one another. The higher the temperature, the faster the atoms or nuclei move. When they collide at these high speeds, they overcome the force of |
Figure 13-13 Plasma Occurrence |
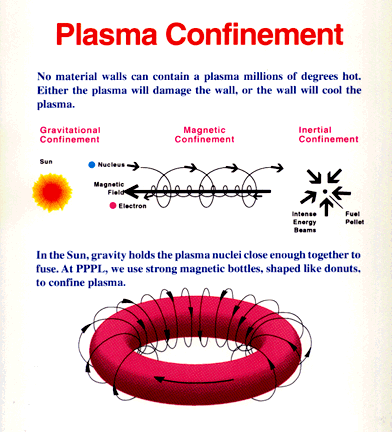
Figure 13-14a Plasma Con- |
repulsion of the positive charges, and the nuclei fuse. In such collisions, energy is released. The |
|
difficulty in producing fusion energy has been to develop a device which can heat the deuterium-tritium1 fuel to a sufficiently high temperature and then confine it for a long enough time so that more energy is released through fusion reactions than is used for heating.
In order to release energy at a level of practical use for production of electricity, the gaseous deuterium-tritium fuel must be heated to about 100 million degrees Celsius. This temperature is more than six times hotter than the interior of the sun, which is estimated to be 15 million degrees Celsius. Scientists have already passed the task of achieving the necessary temperatures. In some cases, they have attained temperatures as high as 510 million degrees, more than 20 times the temperature at the center of the sun. The problem is how to confine the deuterium and tritium under such extreme conditions. A part of the solution to this problem lies in the fact that, at the high temperatures required, all the electrons of light atoms become separated from the nuclei. The fuel is in a plasma state. Because of the electric charges carried by electrons and ions, a plasma can, in principle be confined by a magnetic field. In the absence of a magnetic field, the charged particles in a plasma move in straight lines and random directions. Since nothing restricts their motion the charged particles can strike the walls of a containing vessel, thereby cooling the plasma and inhibiting fusion reactions. In a tokamak, the high-temperature plasma are confined by the magnetic field around the doughnut-shaped nuclear reactor as shown in | the lower section of Figure 13-14a.
However, long-lived pinched plasmas are extremely difficult to maintain. The plasma column is observed to break up rapidly. The reason for the disintegration of the column is the growth of instabilities. The column is unstable against various departures from cylindrical geometry. Small distortions are amplified rapidly and destroy the column in a very short time. The mechanisms of instability in plasma physics are nearly unlimited. Some instabilities are comparable to examples borrowed from fluid mechanics, as the Rayleigh Taylorís instability, which consists of superposing two fluids with the heaviest on top. Imagine for example a vessel in which you pour water and then carefully add oil over the top. The system is then in a state of meta-stable equilibrium. The slightest nudge will provoke a change with the heavier fluid dropping to the bottom, which corresponds to a stable equilibrium. Another type of instability are kink instabilities, which occur when a current parallel to the magnetic field cause twisting of the field lines, recalling the effect obtained if we twist a rope too much: the rope twists out and kinks. The sausage or neck instability causes a greater inwards pressure at the neck of a constriction. This serves to enhance the existing distortion. The Tokamak Fusion Test Reactor has produced significant quantities of fusion power (up to 10 Million Watts) from the fusion of DT (Deuterium and Tritium). However, this has not yet equaled the input heating power -- the breakeven condition. |
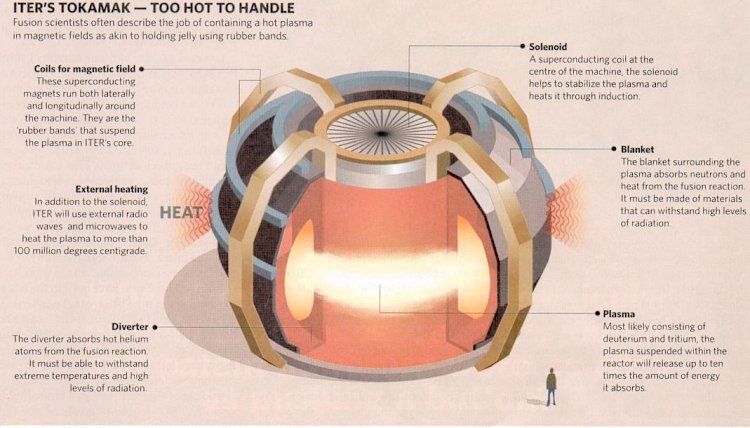 | ITER's six international partners could be in place by the winter of 2005, allowing construction to begin in 2006, and operation in 2016. ITER is designed to heat hydrogen to hundreds of millions of degrees centigrade, and then squeeze energy from the resulting plasma, while holding it stable for minutes at a time. It is based on the tokamak model, which up until today has only one machine that has begun to approach the "break-even point". It is believed that by building a tokamak with bigger size, it will allow the high-temperature high-pressure plasma to remain stable longer (~ 7-10 minutes) producing 500 megawatts of energy within the interval. | |
Figure 13-14b ITER |
 |
Physics and Computer science have combined to create a new field: quantum computing and quantum information. The spark that ignited world wide interest in this new field sprang forth in 1994 with Peter Shor's discovery of a theoretical way to use quantum mechanical resources to unravel a mathematical problem at the heart of electronic commerce and cryptography.
Basic steps towards the creation of a quantum computer have been taken, with the demonstrations of elementary data storage and manipulation using photons and atoms or trapped ions as the quantum bits, or "qubits". Recently, it has been shown that it is possible to build solid-state qubits made from tiny samples of superconducting material. Figure 13-15 shows some of the subjects, which are currently being investigated in the field of quantum computing. |
Figure 13-15 Qunatum Computing |
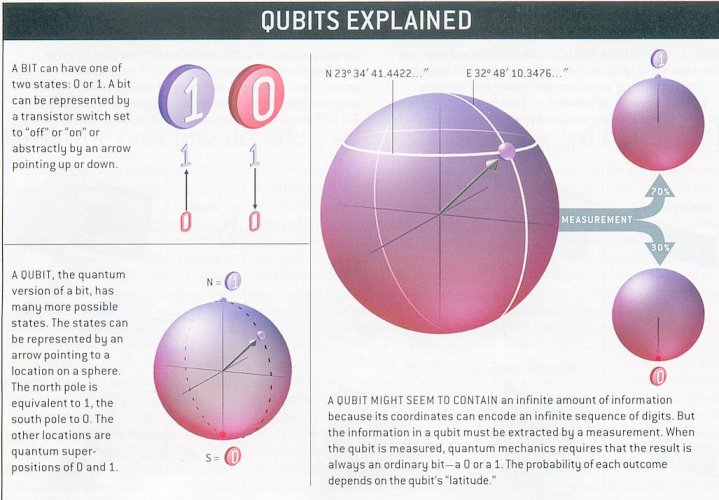 |
Qunatum computing exploits two resources offered by the laws of quantum mechanics: the principle of superposition of states and the concept of entanglement. Superposition is a "one-particle" property; while entanglement is a characteristic of two or more particles. Consider a particle with spin such as the electron. With reference to a given axis (say along the z axis), the spin of the particle can point in two opposite directions, say "up" and "down", and the spin states can be denoted as |1 > and |0 >. But by the laws of quantum mechanics, the particle can exist in a superposition of these two states, corresponding to arbitrary orientation as shown in Figure 13-16. |
Figure 13-16 Qubit [view large image] |
|
Mathematically, the superposition of these two states can be written as: |f > = a |1 > + b |0 > ------ (1) where a and b are related to the probability of finding the electron in state |1 > and |0 > respectively satisfying |a|2 + |b|2 = 1. This normalization defines the total probability of finding the electron to be 1. In general, the |1 > and |0 > states can be represented by any two-states entity such as "on" and "off", horizontal and vertical polarization of a photon, one particle vs no particle, ... etc. |
|f > is called a qubit. If a photon in state |f > passes through a polarizing beamsplitter -- a device that reflects (or transmits) horizontally (or vertically) polarized photons -- it will be found in the reflected (or transmitted) beam with probability |a|2 (or |b|2). Then the general state |f > has been projected either onto |1 > or onto |0 > by the action of the measurement (sometimes it is referred as collapse or decoherence of |f >). Thus according to the rule of quantum mechanics, a measurement of the qubit would yield either |1 > or |0 > but not |f >.(See Figure 13-16.) |
 |
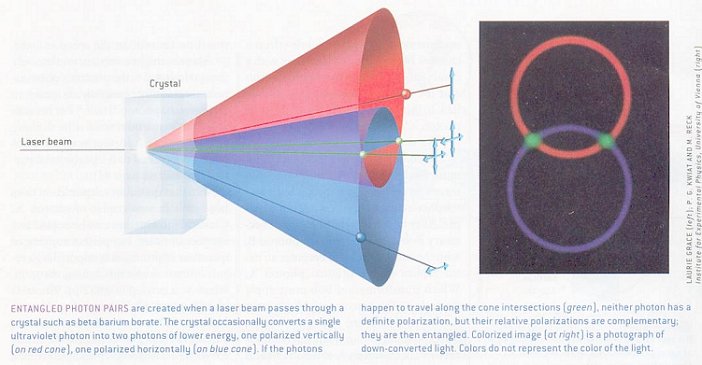 |
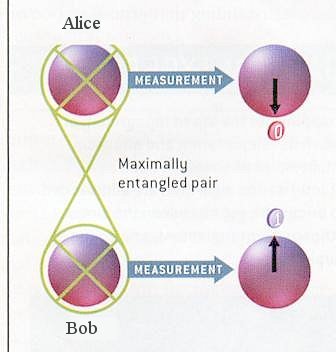
Now, consider a two-particle state: there are four "basis states", |1 >1|1 >2, |0 >1|0 >2, |1 >1|0 >2 and |0 >1|1 >2, where the subscript indicates particle 1 and 2. Again, superpositions can be made of these states, including in particular, the four "maximally entangled Bell states": |1 >1|1 >2 + |0 >1|0 >2 ------ (2) |1 >1|1 >2 - |0 >1|0 >2 ------ (3) |
Figure 13-17 Entanglement [view large image] |
Figure 13-18 Entanglement Implementation |
|1 >1|0 >2 + |0 >1|1 >2 ------ (4) |1 >1|0 >2 - |0 >1|1 >2 ------ (5) |
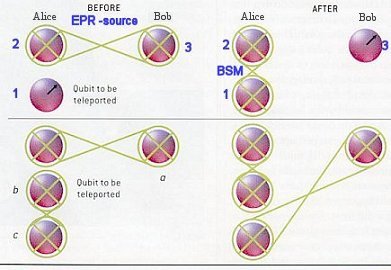 |
Suppose particle 1 which Alice wants to teleport is in the initial state: |f >1 = a |1 >1 + b |0 >1 ------ (6) and the entangled pair of particles 2 and 3 shared by Alice and Bob is in the state: |f >23 = (|1 >2|0 >3 - |0 >2|1 >3)/21/2 ------ (7) which is produced by an Einstein-Podolsky-Rosen (EPR) source2. The teleportation scheme works as follows. Alice has the particle 1 in the initial state |f >1 and particle 2. Particle 2 is entangled with particle 3 in the hands of Bob. The essential point is to perform a joint Bell-state measurement (BSM)3 on particles 1 and 2 which projects them onto the entangled state: |
Figure 13-19 Teleportation [view large image] |
|f >12 = (|1 >1|0 >2 - |0 >1|1 >2)/21/2 ------ (8) |
|
This is only one of four possible Bell states into which the two particles can be entangled. The state given in Eq.(8) distinguishes itself from the others by the fact that it changes sign upon interchanging particle 1 and 2. This unique antisymmetric feature plays an important role in the experiment.
According to the rule of quantum physics once particles 1 and 2 are projected into |f >12, particle 3 is instantaneously projected into the initial state of particle 1. (See top portion of Figure 13-19.) This is because when we observe particles 1 and 2 in the state |f >12 we know that whatever the state of particles 1 is, particle 2 must be in the opposite state. But we had initially prepared particle 2 and 3 in the state |f >23, which means particle 2 must be in the opposite state of particle 3. This is only possible if particle 3 is in the same state particle 1 was initially. The final state of particle 3 is therefore: |f >3 = a |1 >3 + b |0 >3 ------ (9) Note that during the Bell-state measurement particle 1 loses its identity because it becomes entangled with particle 2. Therefore the state |f >1 is destroyed on Alice's side during teleportation. The transfer of quantum information from particle 1 to particle 3 can happen instantly over arbitrary distances, | hence the name teleportation. Experimentally, quantum entanglement has been shown to survive over distances of the order of 10 km. In the teleportation scheme it is not necessary for Alice to know where Bob is. Furthermore, the initial state of particle 1 can be completely unknown not only to Bob but to anyone. It could even be quantum mechanically completely undefined at the time the Bell-state measurement takes place. This is the case when particle 1 itself is a member of an entangled pair and therefore has no well-defined properties on its own. This ultimately leads to entanglement swapping. (See lower portion of Figure 13-19, "e-bit" means entangled bit) A complete Bell-state measurement not only give the result that the two particles 1 and 2 are in the antisymmetric state in Eq.(8), but with equal probabilities of 25% we could find them in any one the remaining three Bell states. When this happens, the state of particle 3 is determined by one of these three different states. Therefore Alice has to inform Bob, via a classical communication channel, which of the Bell state result was obtained; depending on the message, Bob leaves the particle unaltered or changes it to the opposite state. Either way it ends up a replica of particle 1. It should be emphasized that even if it can be demonstrated for only one of the four Bell states as discussed above, teleportation is successfully achieved, albeit only in a quarter of the cases. |
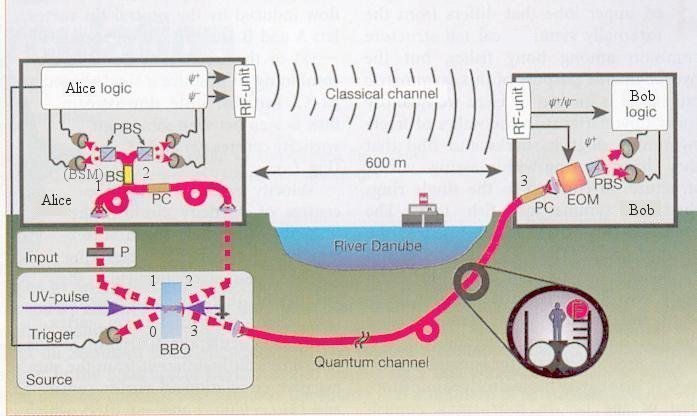 |
polarizing beam splitters (PBS) for Bell-state measurement (BSM). The logic electronics identify the Bell state and convey the result through the microwave channel (RF unit) to Bob's electro-optic modulator (EOM). Depending on the message, it either leaves the photon state unaltered or changes it to the opposite state. Note that because of the reduced velocity of light within the fibre-based quantum channel, the classical signal arrives about 1.5 microseconds before photon 3. Thus, there is enough time to set the EOM correctly before photon 3 arrives. Polarization rotation (which introduces errors) in the fibres is corrected by polarization controllers (PC) before each run of measurements. |
Figure 13-20 Teleportation over River Danube [view large image] |
Polarization stability proved to be better than 10o on the fibre between Alice and Bob, corresponding to an ideal teleportation fidelity of 0.97. |
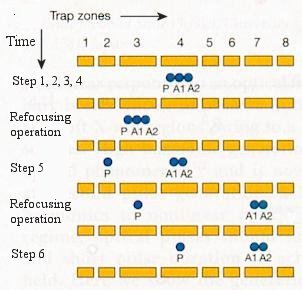 |
Such error-correction protocols have been implemented in 2004 using three beryllium atomic-ion qubits (the qubits comprise the two electronic ground state hyperfine levels, which are equated to the two spin 1/2 states - up and down) confined to a linear, multi-zone trap. It has been demonstrated that fidelity of 0.7 - 0.8 can be achieved in the experiments. However, the method works well only when at most one of the three qubits undergoes a spin-flip error. Figure 13-21 shows the transportation of the ions in the trap during the error-correction protocol as a function of time. Each experiment requires approximately 4 ms to perform. The ions are kept together by careful tuning of the phases of the optical-dipole force. Refocusing operations are required to counteract qubit dephasing caused by fluctuations in the local magnetic field. |
Figure 13-21 Quantum Error Correction [view large image] |
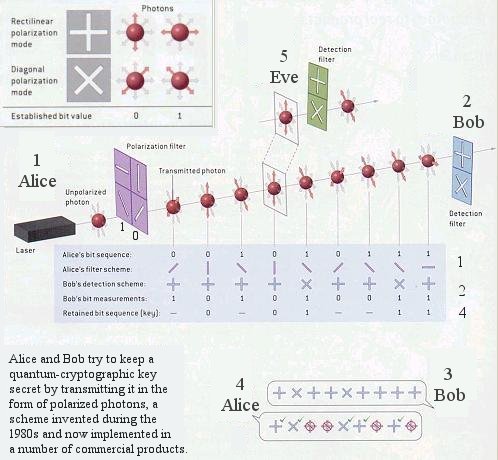 |
Data encryption is used to protect messages and files from prying eavesdroppers. In its simplest form, a coded message can be created in which each letter is substituted with the letter that is two down from it in the alphabet. So "A" becomes "C", "B" becomes "D", ... and so on. The recipient was told that the code (key) is: "Shift by 2". He/she can then decodes the message accordingly. Anyone else will only see a garbled message. Modern encryption employs two keys to provide greater security. The sender selects a public-key such as 1525381, which is the product of two prime numbers: 10667 and 143. This key is used to convert a block of text via an algorithm (a formula for combining the key with the text). The recipent must used a private key such as 143 to decode the encrypted text in the reverse process. The security of public-key cryptography depends on factorization - the fact that it is easy to compute the product of two large numbers but extremely hard to |
Figure 13-22 Quantum Encryption [view large image] |
factor it back into the primes. But the advent of the quantum information era - and, in particular, the capability of quantum computers to rapidly perform monstrously challenging factorizations - may portend the eventual demise of such cryptographic scheme. |