 |
 |
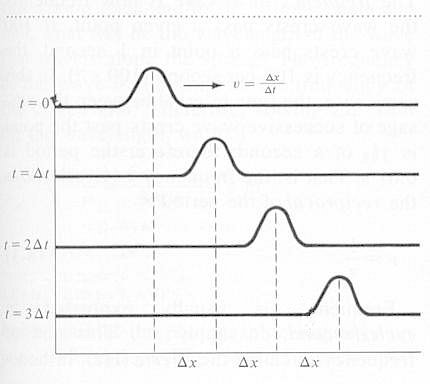
Wave motion is one of the most familiar of natural phenomena. When a medium, whether gas, liquid, or solid, is disturbed, the disturbance moves out in all directions until it encounters a boundary at which point it will either be absorbed, reflected, or refracted depending on the nature of the discontinuity. In reality, the wave would fade away gradually by damping in the medium. The physics of wave motion can be illustrated best in one dimension such as in a string. Figure 01 shows a pulse generated by a single up and down motion of the string. The pulse moves out as shown in successive time frames. Now if the up and down motion of |
Figure 01 Pulse |
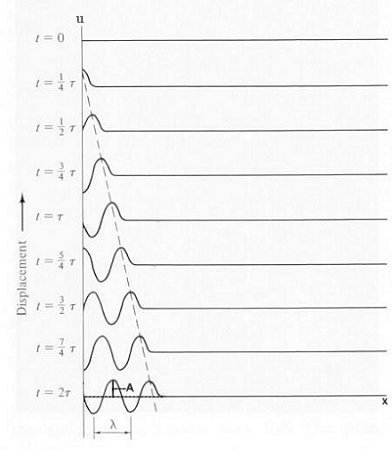
Figure 02 Traveling Wave[view large image] |
the string is driven by a motor, it would generate a traveling wave in the form of the sine function as shown in Figure 02. |
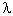 , which is called the wavelength. The frequency of a wave is how frequently the wave crests pass a given point. If 100 wave crests pass a point in 1 second, the frequency is 100 cycle per second (it is sometimes expressed as 100 c/s, or 100 cps, or 100 Hz). The frequency
, which is called the wavelength. The frequency of a wave is how frequently the wave crests pass a given point. If 100 wave crests pass a point in 1 second, the frequency is 100 cycle per second (it is sometimes expressed as 100 c/s, or 100 cps, or 100 Hz). The frequency 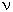 and the period
and the period 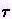 is related by a simple formula:
is related by a simple formula: 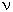 = 1/
= 1/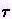 ----------- (10)
----------- (10)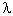
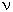 =
= 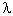 /
/ 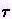 = v, ---------- (11)
= v, ---------- (11)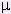 of the medium by yet another formula:
of the medium by yet another formula: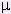 )1/2, ---------- (12)
)1/2, ---------- (12)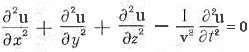 | ---------- (13a) |
 | ---------- (13b) |
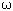 = 2
= 2 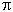
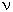 , k = 2
, k = 2 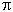 /
/ 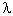 , and A is the amplitude as shown in Figure 02. It can be shown that the cosine function in similar form as Eq.(13b) is also a solution for Eq.(13a) with the initial and boundary conditions of u = A at t =0 and x =0.
, and A is the amplitude as shown in Figure 02. It can be shown that the cosine function in similar form as Eq.(13b) is also a solution for Eq.(13a) with the initial and boundary conditions of u = A at t =0 and x =0.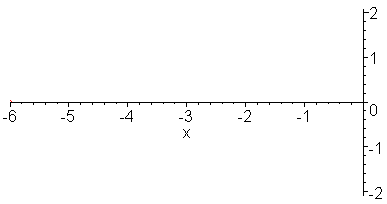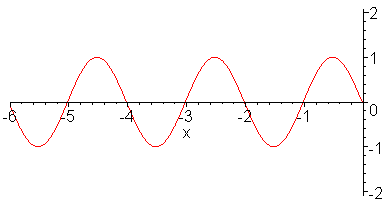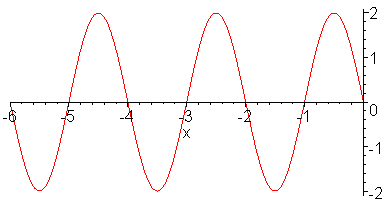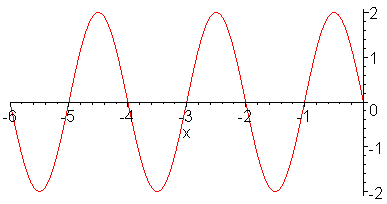 |
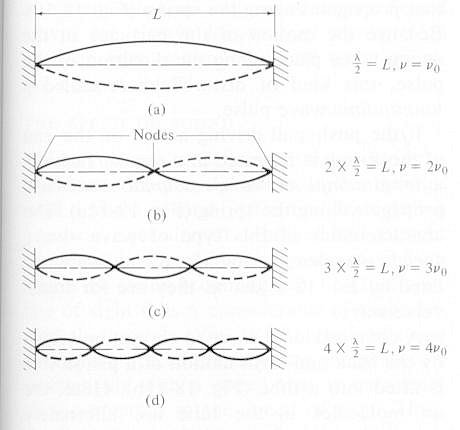 | If the vibrating string is attached to a rigid support at the other end, the traveling wave will be reflected and will begin to travel back toward the driven end. If the frequency of vibration is not properly chosen, the direct wave and the reflected wave will combine to produce a jumbled wave pattern. It is found that only a number of particular frequencies can produce regular patterns of motion along the string. At these frequencies, certain positions along the string remain stationary (the nodes) while the rest of the string vibrates with a constant |
Figure 03 Standing Wave, Animation[view large image] |
Figure 04 Standing Wave |
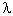 / 2 ), ---------- (14)
/ 2 ), ---------- (14)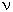 o for the particular string. The higher frequencies with integer multiple 2
o for the particular string. The higher frequencies with integer multiple 2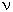 o, 3
o, 3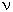 o, and 4
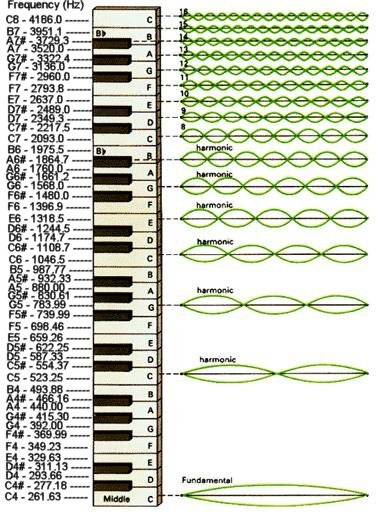
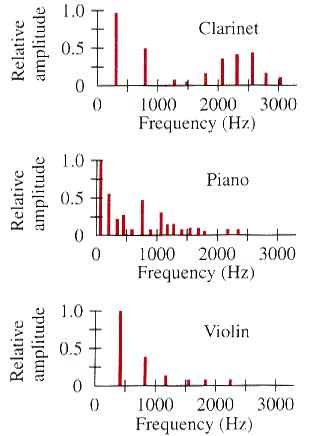
o, and 4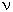 o, ... are called harmonics or overtones. Usually, the dominant standing wave is the fundamental as shown in Figure 11, which displays the proportion of the fundamental to the various harmonics for different kinds of musical instruments. Since Eq.(13a) is a linear differential equation, the sum of the separate solutions is also a solution. Thus, superposition of the the fundamental and harmonics can generate different kind of waveform as shown in Figure 05. Mathematically, it is expressed by the Fourier series f(x) with u = f(x) sin(n
o, ... are called harmonics or overtones. Usually, the dominant standing wave is the fundamental as shown in Figure 11, which displays the proportion of the fundamental to the various harmonics for different kinds of musical instruments. Since Eq.(13a) is a linear differential equation, the sum of the separate solutions is also a solution. Thus, superposition of the the fundamental and harmonics can generate different kind of waveform as shown in Figure 05. Mathematically, it is expressed by the Fourier series f(x) with u = f(x) sin(n vt/L):
vt/L):
 |
 |
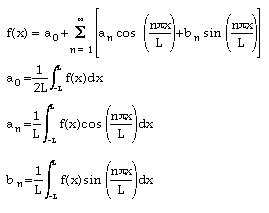 ----- (15) ----- (15) |
Figure 05 Composite Wave [view large image] |
Figure 06 Fourier Series and Waveforms[view large image] |
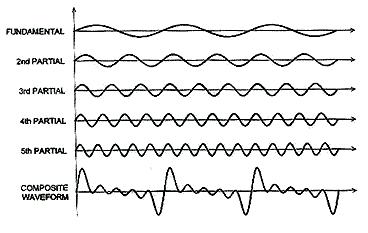
where f(x) is the maximum displacement of the wave at x, L=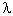 /2 and n = 1, 2, 3, ... Figure 06 depicts the various waveforms produced by the respective Fourier series. /2 and n = 1, 2, 3, ... Figure 06 depicts the various waveforms produced by the respective Fourier series. |
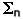 represents a sum over all the variables with an index n. For example,
represents a sum over all the variables with an index n. For example, 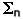 n2 = 12 + 22 + 32 + ... The integral sign
n2 = 12 + 22 + 32 + ... The integral sign 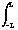 represents a sum over a continuous variable x from x = -L to x = +L. A trivial example is
represents a sum over a continuous variable x from x = -L to x = +L. A trivial example is 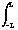 dx = 2L
dx = 2L
 |
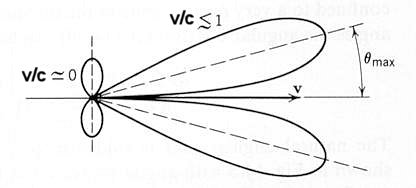 |
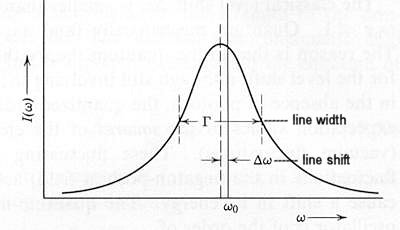
either, Figure 07b shows the radiation pattern for charge accelerated in its direction of motion. The "8" shape pattern (a no hole doughnut in 3 dimension) is emitted at low velocity, while the lobes (a thick cone in 3 dimension) are generated at speed close to the velocity of light. |
Figure 07a Line Broaden- ing [view large image] |
Figure 07b Radiation Pattern [view large image] |
 |
 |
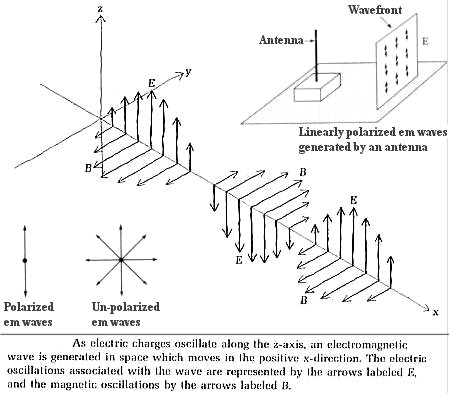
will oscillate in a perpendicular direction. Thermal radiation emitting from large number of incoherent sources (molecules) is unpolarized. Only the radiations from organized motion such as those in antenna transmission, laser, or accelerating electron beam (as in synchrotron radiation) exhibit this polarization effect. Since the electric field can always be resolved into two components perpendicular to each other, in many situations one of these components would be blocked or the optical paths separated by the interacting material. Figure 08b |
Figure 08a Polarization |
Figure 08b Polarized Light |
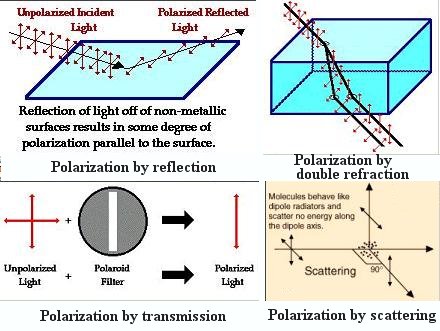
shows the polarization of unpolarized light by reflection (glare), scattering (blue sky, red sunset), transmission (through Polaroid filter), and double refraction (in some crystals such as calcite). |
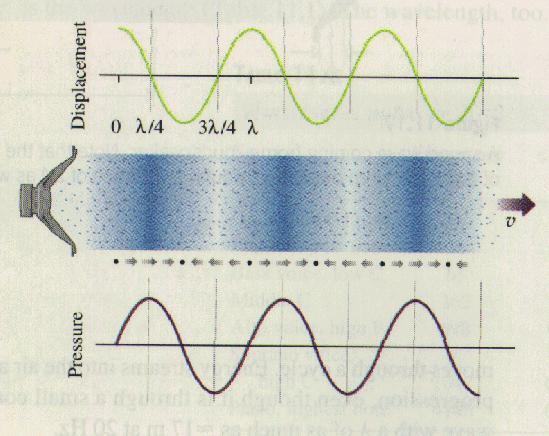 |
A compressional wave in air can be set up by the back-and-forth motion of a speaker as shown in Figure 09. Here, the air molecules are alternately pressed together and pulled apart by the action of the speaker. The result is a propagating wave in which the pressure (and density) of the air varies with distance in a regular way - the pattern is, in fact, exactly the same as the displacement pattern of a transverse wave on a string (see Figure 01 and 02). Compressional waves in air are called sound waves, which are always longitudinal waves with the vibration parallel to the direction of propagation. Most of the previously mentioned concept about waves can be applied to the sound wave without modification except the formula for the wave velocity in Eq. (12) where the tension is replaced by the "bulk modulus" (change in pressure / change in volume) and the linear density is |
Figure 09 Sound Wave |
just the density of the air. It turns out that the velocity of sound at STP is about 330 m/s. |
 |
f = f0 x 2n, ---------- (16) where n = 0, 1, 2, 3, ... describes the octave relationship such as 20 (unison), 21 (one octave), 22 (two octaves), 23 (three octaves), ... Within the range of an octave, there is a series of frequencies called consonant intervals, which is known to produce the most pleasing sounds to the ear. They are usually combinations of notes related by ratios of small integers, such as the fifth (3/2) or third (5/4). Many musical instruments are tuned according to these intervals. Unfortunately, this kind of tuning depends on the scale - the tuning for C Major is not the same as for D Major. The "equal-temperament" scale solves the problem by dividing the octave into twelve equal intervals, each has a size of 21/12 x f, where f is the fundamental or harmonic frequency. It was developed for keyboard instruments, such as the piano, so that they could be played equally well (or badly) in any key. It is a compromised tuning scheme. |
Figure 10 Musical Scale |
| Note | Syl- lable |
Consonant Interval | Ratio | Decimal | E-T Interval (n)/(¢) | E-T Scale, 2n/12 | Difference/(in ¢) |
|---|---|---|---|---|---|---|---|
| C | Do / 1 | octave (fundamental) | 1/1 | 1.000000 | n = 0 / 000 | 1.000000 | 0.000000 / 00.0 |
| C# | minor second | 25/24 | 1.041667 | n = 1 / 100 | 1.059463 | -0.017796 / -29.3 | |
| D | Re / 2 | major second | 9/8 | 1.125000 | n = 2 / 200 | 1.122462 | +0.002538 / +3.91 |
| D# | minor third | 6/5 | 1.200000 | n = 3 / 300 | 1.189207 | +0.010793 / +15.6 | |
| E | Mi / 3 | major third | 5/4 | 1.250000 | n = 4 / 400 | 1.259921 | -0.009921 / -13.7 |
| F | Fa / 4 | fourth | 4/3 | 1.333333 | n = 5 / 500 | 1.334840 | -0.001507 / -1.96 |
| F# | diminished fifth | 45/32 | 1.406250 | n = 6 / 600 | 1.414214 | -0.007964 / -9.78 | |
| G | So / 5 | fifth | 3/2 | 1.500000 | n = 7 / 700 | 1.498307 | +0.001693 / +1.96 |
| G# | minor sixth | 8/5 | 1.600000 | n = 8 / 800 | 1.587401 | +0.012599 / +13.7 | |
| A | La / 6 | Major sixth | 5/3 | 1.666666 | n = 9 / 900 | 1.681793 | -0.015127 / -15.6 |
| A# | minor seventh | 9/5 | 1.800000 | n = 10 / 1000 | 1.781797 | +0.018203 / +17.6 | |
| B | Ti / 7 | major seventh | 15/8 | 1.875000 | n = 11 / 1100 | 1.887749 | -0.012749 / -11.7 |
| C | Do / 1 | Octave (1st harmonic) | 2/1 | 2.000000 | n = 12 / 1200 | 2.000000 | 0.000000 / 00.0 |
| Loudness | Intensity (watts/m2) | Intensity Level (dB) |
|---|---|---|
| Threshold of hearing | 10-12 | 0 |
| Rustle of leaves | 10-11 | 10 |
| Whisper | 10-10 | 20 |
| Watch ticking at 1 m | 10-9 | 30 |
| Radio (low) | 10-8 | 40 |
| Quiet conversation | 10-7 | 50 |
| Quiet motor at 1 m | 10-6 | 60 |
| Busy street traffic | 10-5 | 70 |
| Door slamming | 10-4 | 80 |
| Heavy truck, 50 ft | 10-3 | 90 |
| Power mower | 10-2 | 100 |
| Pneumatic drill | 10-1 | 110 |
| Near aeroplane engine | 1 | 120 |
| Physical damage | 10 | 130 |
 |
[view large image] |
Figure 11 Timbre |
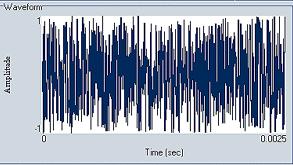 |
Noise sound contains so many harmonics randomly distributed throughout the spectrum that it doesn't have a perceivable pitch. Noise is a sound that is not periodic. That is, it contains random elements that cannot be described as a regular series of sine wave components. The name white noise is given to this sound: noise because of the lack of order in it, and white because it contains frequencies from all over the audible spectrum. Nevertheless, noise is extremely important in music. Most percussion instruments contain a great deal of noise. Radio static, rainfall, wind, thunder, jet exhaust, etc. are some examples of non-musical noise. Figure 12 shows the random amplitude of noise over an interval of time. |
Figure 12 Noise |
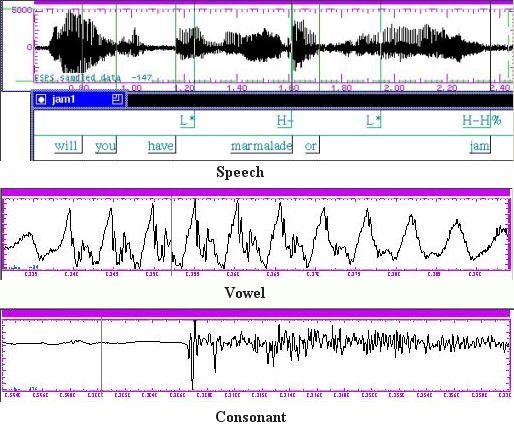 |
Speech has a definite pattern such as the pronunciation of "will you ..." etc. (see Figure 13) -- but little regularity. Both speech and white noise contain transient sounds -- that is, air motion that doesn't repeat. The difference is that speech uses these non-repeating sounds in recognizable patterns, whereas white noise has no distinct patterns at all. In essence, speech is order without regularity. Alternatively, speech can be considered as a mixture of transient sounds and quasi-periodic sounds corresponding to consonants and vowels, respectively (a vowel is a sound in spoken language that is characterized by an open configuration of the vocal tract, in contrast to consonants, which are characterized by a constriction or closure at one or more points along the vocal tract). Singing emphasizes the vowels, which being quasi-periodic (see Figure 13), are tailor-made for musical creations. Speech tends to emphasize consonants much more than singing. Singers, |
Figure 13 Speech, Vowel, and Consonant [view large image] |
especially operatic singers, are often very hard to understand because that type of singing requires a very heavy and unnatural concentration on the vowels. |
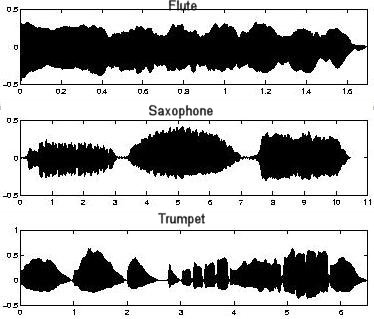 |
When periodic air disturbances happen less than 16 times a second, we hear them as individual clicks, pops, or other events. An interesting thing happens, though, when those repetitions come faster than 16 times a second. There is a breakdown in the process because our nervous system cannot deal with hearing more than 16 individual events in a second, and begins to hear all of those disturbances as a single event -- a musical note. The faster the disturbance, the higher pitch we hear. Over the last few thousand years, we have been building some highly sophisticated devices that disturb the air at precisely controlled rates. We normally call these devices "musical instruments". Music has been defined as "ordered non-speech sound". There is a very close relationship between speech and the melodic and rhythmic elements of singing, which is just a slight modification of speech. In short, the amount of order and pattern we perceive in air disturbances determines |
Figure 14 Musical Patterns [view large image] |
whether we hear noise, speech, music, or anything in between. Sound patterns over a time interval for some musical instruments are depicted in Figure 14. |
 |
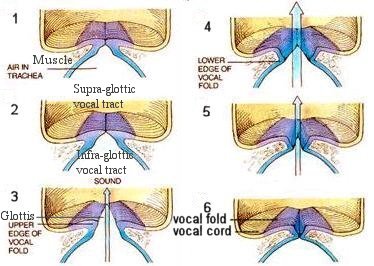 |
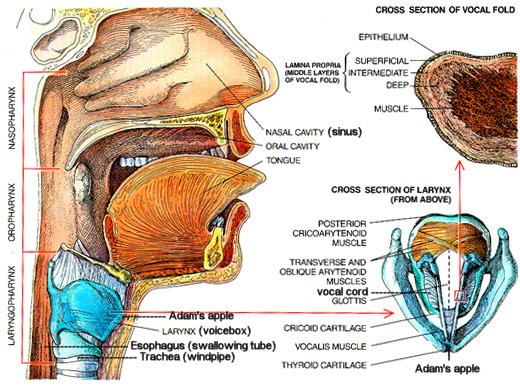
Human voices are generated in the larynx, commonly called the voicebox. It is situated inside the bump on the throat called the "Adam's apple" (see Figure 15). The larynx is a multi-function organ used for swallowing, breathing, or talking. The larynx contains a membrane composed with the "vocal cords" (a misnomer) and the "vocal folds". When we breathe, the vocal folds relax and air moves through the space between them without making a sound. When we talk, the vocal folds tighten |
Figure 15 Larynx |
Figure 16 Voice Production [view large image] |
up and move closer together. Air from the lungs is forced between them and makes them vibrate, producing the sound of our voice. A loud sound will be |
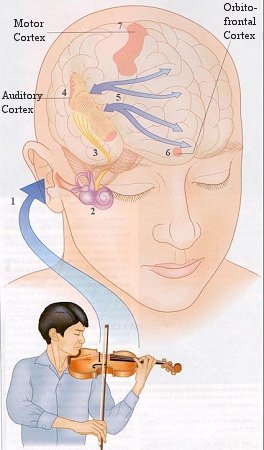 |
Music provides a tool to study numerous aspects of neuroscience, from motor-skill learning to emotion. Indeed, from a psychologist's point of view, listening to and producing music involves a tantalizing mix of practically every human cognitive function. Even a seemingly simple activity, such as humming a familiar tune, necessitates complex auditory pattern-processing mechanisms, attention, memory storage and retrieval, motor programming, sensory-motor integration, and so forth.
|
Figure 17 Music and Neuro- science [view large image] |
 |
|
Figure 18 Music and Dance [view large image] |
stimuli, such as food or sexual stimuli. It is thought that perhaps music, and all art in a way, manages to transcend mere perception because it contacts our more primordial neurobiology. |