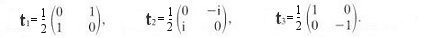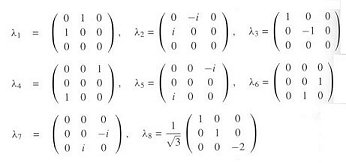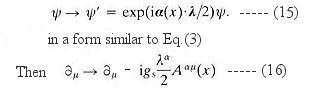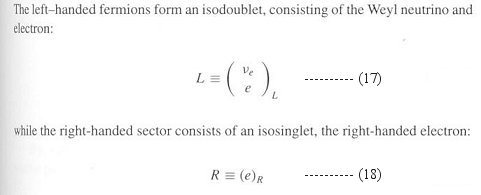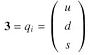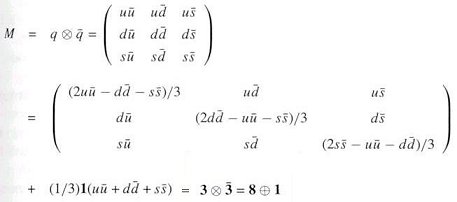Abelion/non-Abelion, and the U(1), SU(2), SU(3) Groups

Abelion/non-Abelion Groups
The Mathematics of U(1), SU(2), and SU(3) Groups
Application to Elementary Particles

Abelion/non-Abelion Groups

If a and b are both members of the group G, then their product, c = ab is also a member of the group G.
The process is associative, i.e., a(bc) = (ab)c.
There must be an element, called the unit element and usually denoted by e, defined so that ae = a, be = b, and so on for all elements in the group.
Each element has an inverse, written as a^-1, b^-1 and so on, defined so that aa^-1 = e and so on.

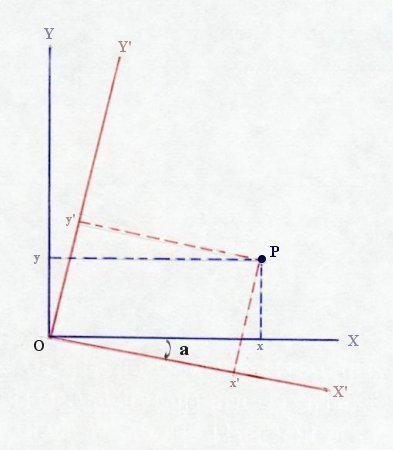
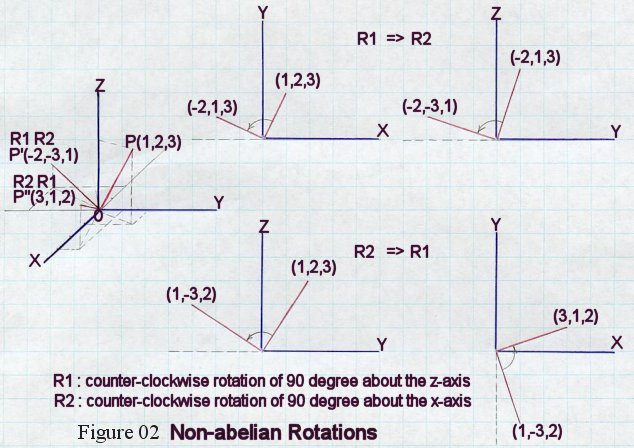
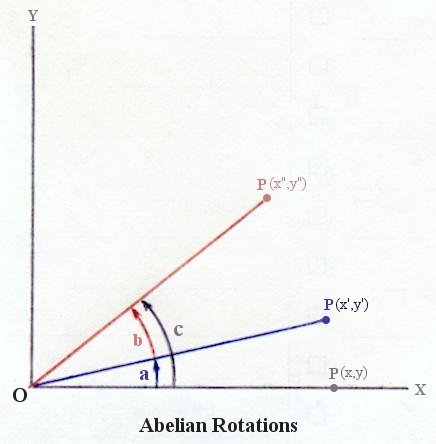
A group for which ab = ba is an Abelian group. The set of ordinary integer numbers ( ... -3, -2, -1, 0, 1, 2, 3, ...) under "addition" is a simple example of an Abelian group, where "0" is the unit element and the inverse is the same number with opposite sign.

Figure 01a 2-D Rotation [view large image]

Another example is the two-dimensional rotation shown in Figure 01a. The angular displacement c is the sum of the rotations a and b, the unit element is a rotation of 0^o, and the inverse is a rotation in the opposite direction. Because the angle of rotation can be infinitesimally small, this kind of group is called a continuous group. For better comprehension of the mathematical formula, Figure 01b shows the coordinate system rotates by an angle a about the origin O instead of rotating the point P. The transformation formula between (x,y) and (x',y') can be written as:

x' = [cos(a)] x - [sin(a)] y ---------- (1)
y' = [sin(a)] x + [cos(a)] y ---------- (2)

Figure 01b Coordinate Rotation [view large image]

The fact that the laws of physics are unchanged by such a rotation implies conservation of the z component of angular momentum; in general, whenever the physical law is invariant under the operation of a symmetry group, there must be some conserved quantity associated with that operation. This is sometimes referred to as Noether's theorem, and is a useful feature of group theory, which can be used to provide physical insights into the behaviour of interactions and particles such as whether the process is permissible or if an entity is missing without knowing the detailed dynamic. When this rotation group is applied to the "internal space" in quantum electrodynamics, the global operation (same amount of internal rotation everywhere) leads to the conservation of electric charge; while the local operation associates a gauge boson (the photon) with the electromagnetic interaction. The rotation group in real space is called SO(2) operating on a two-dimensional space; while the one for the "internal space" is called U(1) because the "two-dimensional space" has been transformed to an equivalent complex number, e.g., z = x + iy.

The elements in a non-abelian group do not commute as shown in Figure 02 where the two consecutive 90^o rotations R1 R2 generates a completely different result from R2 R1 with the order reversed. The original vector OP with P at (1,2,3) moves to P' at (-2,-3,1) after applying R1 R2; while it ends up at P'' (3,1,2) after applying R2 R1. In general, there are three degrees of (rotation) freedom corresponding to rotation about the x, y, and z axis respectively. This 3-dimensional rotation group in real space is called SO(3). The equivalent 3-dimensional rotation group in "internal space" is called
SU(2) with three "phase angles" (parameters) associated to three non-commuting matrix operators.
[view large image]

As far as only the (residual) strong interaction is concerned, the neutron and proton can be considered as the two states of the "isospin". This system is invariant under the operation of the SU(2) group globally, and leads to two constants of motion: the square of the total "isospin" and the z-component of the "isospin". It is found that if the SU(2) group is applied locally to the electroweak interaction with a system of electron and neutrino (or up and down quarks), three gauge bosons (corresponding to the three parameters) are required to render the system invariant under such operation. The proposed gauge bosons have been found and the electroweak theory has been validated by many experiments.

[Top]

The Mathematics of U(1), SU(2), and SU(3) Groups

Let's consider the phase transformation of a complex function (with real and imaginary parts):

f' = e^ia f ---------- (3)
where the phase angle a is a constant for a global transformation. It is a function of (x,y,z,t) for local transformation.

If f and f' are decomposed into the real and imaginary parts: f = f_R + i f_I ---------- (4)

Then Eq.(3) can be re-written as:

f'_R = [cos(a)] f_R - [sin(a)] f_I ---------- (5)
f'_I = [sin(a)] f_R + [cos(a)] f_I ---------- (6)

which is in the same form as Eqs.(1) and (2) for the 2-dimensional rotation, but in the f_R - f_I plane, whose 'coordinates" are the real and imaginary parts of the function. This plane is called an internal space, and the associated symmetry an internal symmetry.

Two successive transformations such as: f => f' => f" ---------- (7)
where f" = e^ib f', can be written in the form:

f" = e^i(a+b) f = e^ic f ---------- (8)
with c = a + b. This is a transformation of the same form as the original one. The set of all such transformations forms what mathematicians call a group, in this case U(1), meaning the group of all "unitary" one-dimensional matrices. A unitary matrix U is one such that

UU⁺ = U⁺U = I ---------- (9)
where I is the identity (unity matrix) and "⁺" denotes the Hermitian conjugate (defined such that the mean value of an operator is real). Eq.(9) is required for preserving the normalization (probability). The transformation of the U(1) group have the simple property that it does not matter in what order they are performed, i.e., a + b = b + a. Thus U(1) = e^ia = e^{ia^.(1)} = e^{ia^.I}
is called an Abelian group in which different transformations commute. Since the phase angle can be infinitesimally small, this kind of group also belongs to the Lie group which is important in investigating physical system.

In SU(2) the phase angle a = a^.I is replaced by a^.t with a = (a₁, a₂, a₃) - there are now three phase angles, and three 2x2 non-commuting matrices (generators) for t (the matrices are known as the Pauli matrices):

---------- (10)

For the non-Abelion groups, the number of phase angles (parameters) is determined by the formula N_a = n² - 1, where n is the dimension of the internal space, e.g., N_a = 3 for n = 2 in SU(2).

It can be shown that the absolute square for the determinant of U is 1, i.e., |detU|² = 1. Thus |detU| can be either +1 or -1. The "S" in "SU" means the transformations are "Special" satisfying |detU| = +1, which implies continuous roatations without reflections. Therefore SU(2) designates the group of special, unitary 2x2 matrices.

In SU(3) there are eight phase angles and eight 3x3 non-commuting matrices (generators):

---------- (11)

The SU(2) and SU(3) transformations are more like the non-commuting 3-dimensional rotations of real space because of the non-commuting generators, e.g., a t₁ + b t₂ ¬= b t₁ + a t₂. These groups are called non-Abelian for this reason.

If we define t² = t₁² + t₂² + t₃² + ... ---------- (12)

It can be shown that the phase transformations are characterized by the eigenvalue of t² and t₃ with eigenvector |t,m>:

t² |t,m> = t(t+1) |t,m> ---------- (13)
t₃ |t,m> = m |t,m> ---------- (14)
where t is determined by the formula n = 2t +1 (n is the dimension of the generator) and for a given t, the value of m can be -t, -t+1, ..., t-1, t; i.e., there are 2t+1 degenerate states for a given t. For example, in the case of SU(2) n = 2 yields t = 1/2, and m = -1/2 or +1/2.

[Top]

Application to Elementary Particles

In quantum field theory, if we demand the system to be invariant under the local phase (or gauge) transformation such as:

where A is the field for the gauge bosons, g_s is the coupling constant, lambda is the generator. The second term in Eq.(16) is responsible for the various interactions via the exchange of bosons (see Eq.(38) in "Quantum Field Theory"). The number of gauage bosons depends on the dimension of the generator. Thus, there is only the photon for the U(1) group applicable to electromagnetic interaction; there are three vector bosons - W⁺, W^-, and Z^o for the SU(2) group applicable to weak interaction; and there are eight gluons for the SU(3) group applicable to strong interaction (see Table 15-03).

Now let's turn to the physical interpretation of the complex function in Eq.(3). For the U(1) group this function can be associated with the two component nucleon doublet (p, n), if we equate f_R = p and f_I = n, where p and n represent the wave function for the proton and neutron respectively. It was thought that the proton and neutron are the same particle in different state - p with a positive charge and isospin +1/2, while n is neutral with isospin -1/2. The dynamic of these particles are described by the Klein-Gordon Equation. Another case applies to the two-component electron wave function (e_L, e_R) representing the left-handed and right-handed states (antiparallel and parallel spin to the momentum direction as m => 0 or
v => c) respectively. The dynamic of these particles are described by the Dirac Equation.

Application of the SU(2) group to weak interaction is more complicated because of parity violation. Since there is no right-handed neutrino, the wave functions are split into a left-handed and right-handed parts:

There exists an empirical relation of Gell-Mann and Nishijima for the electric charge of a particle, namely:

Q = t₃ + (Y/2) ---------- (19)
where Q is the charge, t₃ is the third component of the generator, and Y is the "hypercharge".

To satisfy this formula for electro-weak interaction with SU(2) X U(1) symmetry where the SU(2) group splices together with the U(1) group (no mixing), L has to be an eigenvector of SU(2) with t = 1/2 and R an eigenvector of U(1) with t = 0. Similar assignment can be given to the u (up), d (down), and s (strange) quarks as listed in the table below:

Particle	Q	t	t₃	Y
v_e	0	1/2	1/2	-1
e_L	-1	1/2	-1/2	-1
e_R	-1	0	0	-2
u	2/3	1/2	1/2	1/3
d	-1/3	1/2	-1/2	1/3
s	-1/3	0	0	-2/3

Table 01 Gell-Mann-Nishijima Relation

where Y = S + B for the quarks with S for the strangeness number, B for baryon number, which is equal to +1/3 for quark and -1/3 for anti-quark.

In strong interaction the wave functions for the quarks u, d, and s constitute the fundamental representation of SU(3):

---------- (20)

Beginning with the fundamental representation in Eq.(20), all representations of SU(N) can be generated by taking the multiple (tensor) products. For example, the bound states of mesons can be constructed according to the following scheme:

---------- (21)

where the bar "^-" denotes anti-particle.

Table 02 lists the relation between the meson wave functions and the quark pairs. The value within the brackets is the rest mass in Mev.

where J is the total angular momentum quantum number. The mesons in the middle column belongs to J = 0, while those in the right column belongs to J = 1. In terms of the meson wave functions the octet in Eq.(21) can be re-written in the form of
Eq.(22). Similarly, the baryon wave functions are related to the quark triplet as shown in Table 03 and Eq.(23).

This is the Eightfold Way originally proposed by Gell-Mann and Neman in 1961. The mass splitting is caused by various interactions as shown in Figaure 03 below:

Note: These elementary particles were referred to as resonances in the 1960s. Now they are considered as the excited states of hadrons with some of their constituent quarks boosted into higher higher energy levels. Most of them have a very short lifetime about 10^-23 sec.