Neutrino Mass
Contents
The Missing Neutrinos
Detection of Neutrino Mass
Implications
 |
 |
Back in the 1950s it was generally believed that neutrino has no mass and it exists only as a left-handed neutrino or right-handed anti-neutrino (see Figure 01) participating in weak interaction. Later on it is found that there are three different flavors of neutrino as shown in Figure 15-04
|
|
|
However, it seems that something is missing. For more than 30 years, scientists have been capturing electron-neutrinos generated by nuclear fusion in the Sun. These observations have always counted fewer neutrinos than the best models predict.
From the impact of cosmic ray on a nucleus in the atmosphere it is expected that the ratio of muon-neutrinos to electron-neutrinos is 2 to 1. The observation has a shortfall of muon-neutrinos with a ratio of about 1.3 to 1.
[Top]
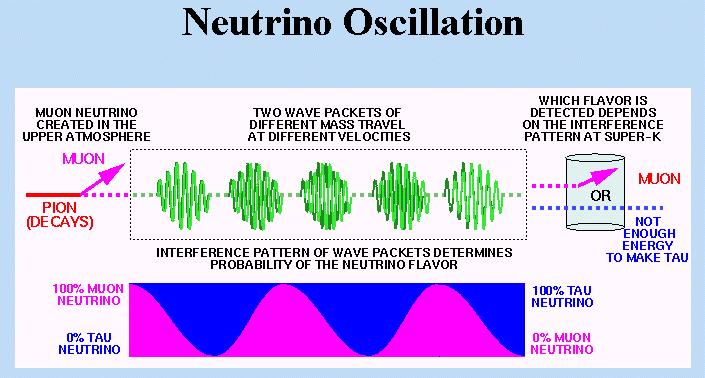
This problem of missing neutrinos can be resolved if the neutrinos has mass. In this case, the existence of a neutrino can oscillate between the flavors as shown in Figure 02. According to quantum mechanics, the neutrino can be represented by two wave packets corresponding to the two flavors propagating at different speeds. Thus the interference pattern varies along the traveling path with different ratio (of the flavors) at any particular point.
According to the Standard Model, neutrino mixing is expressed mathematically by the CKM matrix as shown in Figure 03, where the mixing angles  ( ij = 12, 13, 23) and the phase angle
( ij = 12, 13, 23) and the phase angle  are four parameters determining the amount of mixing and CP violation respectively, where
are four parameters determining the amount of mixing and CP violation respectively, where 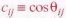 , and
, and 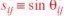 . The neutrino states on the left of the equation are the flavor states
. The neutrino states on the left of the equation are the flavor states
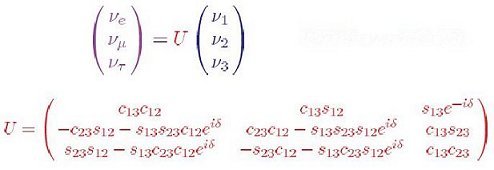 |
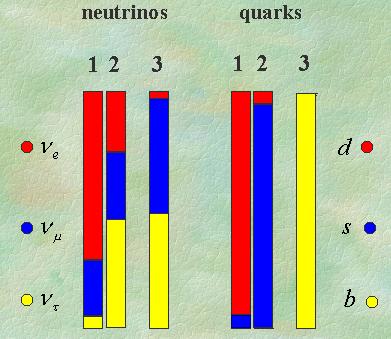 |
produced in weak interaction, while the states on the right (with the numerical subscripts) are called the mass states corresponding to free neutrino with different mass. Neutrino mixing is large in comparison to the quark mixing as shown in Figure 04. The origin of mixing is not explained by the Standard Model.
|
|
|
 |
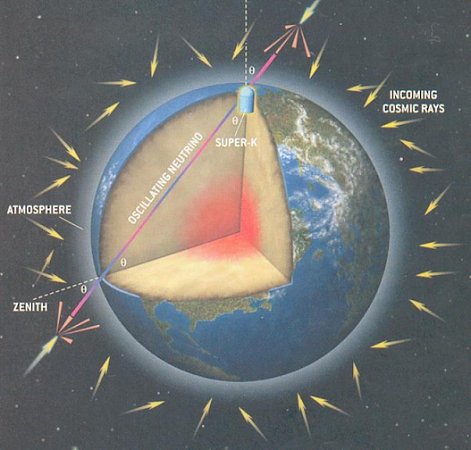 |
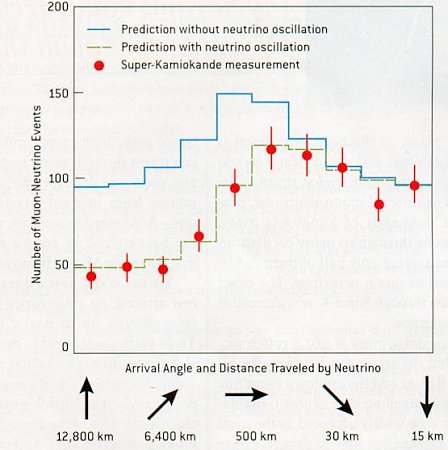
Figure 05 shows the agreement between the Super-K measure- ment and theory with neutrino oscillation. The neutrino in the upward direction would have to travel as long as 13,000 km, i.e., the diameter of the Earth. The horizontal direction would be about 500 km, i.e., the distance to the edge of the atmosphere (see Figure 06). The Sudbury Neutrino Observatory (SNO) in Ontario measured the total number of neutrinos from the Sun as well as the number of electron-neutrinos alone, and it shows that the total is much greater. The accounting seems to balance according to oscillation.
|
|
|
|
The probability of oscillation between 2 types of neutrinos (for example, 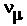 and
and 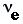 ) is given by the relation:
) is given by the relation:
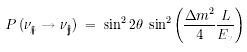
where  =
=  ij is the mixing angle, L is the distance traveled by the neutrino, E stands for the energy of the neutrino, and
ij is the mixing angle, L is the distance traveled by the neutrino, E stands for the energy of the neutrino, and
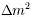 =
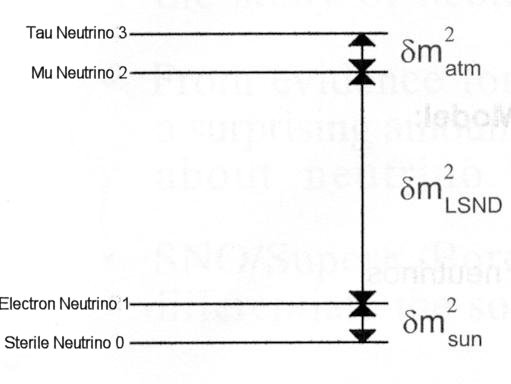
= 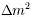 ij = mj2 - mi2 is the difference of the mass square. The mixing angles are determined from the amplitudes of the oscillation. The
ij = mj2 - mi2 is the difference of the mass square. The mixing angles are determined from the amplitudes of the oscillation. The 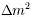 ijs can be calculated from the periods.
ijs can be calculated from the periods.
 |
The solar neutrino measurements by SNO yields  12 ~ 30o, and 12 ~ 30o, and 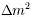 21 = 5x10-5 ev2. 21 = 5x10-5 ev2.
While those from Super-K gives  23 ~ 45o, and 23 ~ 45o, and  32 = 3.5x10-3 ev2. 32 = 3.5x10-3 ev2.
The short-baseline LSND experiment measured the oscillation of 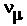 into into 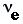 . It yields . It yields 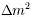 ~ 1 ev2 and ~ 1 ev2 and  ~ 0o, which is very different from the other measurements. A sterile neutrino is required to reconcile all the data as shown in Figure 07. Other experiments indicates ~ 0o, which is very different from the other measurements. A sterile neutrino is required to reconcile all the data as shown in Figure 07. Other experiments indicates  13 and the phase angle 13 and the phase angle  ~ 0o. ~ 0o.
|
|
These data indicate large mixing between neutrinos (in comparison to quark) and small mass (at least million times smaller relative to electron's). But the data do not provide absolute mass measurement for the neutrinos. Direct measurements of the absolute neutrino mass impose the upper bounds: 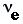 < 2.2 ev,
< 2.2 ev, 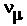 < 190 kev, and
< 190 kev, and 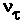 < 18.2 Mev.
< 18.2 Mev.
[Top]
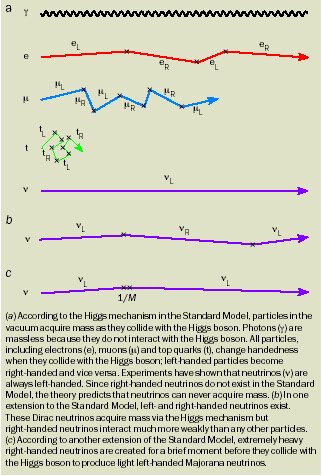 |
- Majorana Neutrino - As shown in (a) of Figure 08, the original Standard Model considers neutrino as massless and exists in the form of left-handed neutrino or right-handed anti-neutrino. In addition, these two kinds are distinguished by the lepton number (for both electron and neutrino) L, which is +1 for neutrino and -1 for anti-neutrino. The lepton number is conserved in weak interaction according to the Standard Model. Since the neutrino has no charge, the lepton number is the only indictor to differentiate a neutrino from an anti-neutrino. When neutrino has mass, its speed would always be lower than the speed of light, theoretically an observer can move in a speed faster than the left-handed neutrino, overtakes this neutrino and sees a right-handed one. For the case when the lepton number is not conserved, there is no way to distinguish the neutrino and the anti-neutrino. The observer can claim that the left-handed neutrino turns into a right-handed anti-neutrino at the moment of "overtaking". This lepton number violating neutrino is called Majorana neutrino named after the originator.
|
|
- The Dirac Mass - The simplest way to introduce neutrino mass into the Standard Model is to add a neutrino mass term via the same Higgs mechanism for the electron and quark. The right-handed neutrino (sterile neutrino) is assigned to the isosinglet (with weak isospin 0) similar to the right-handed electron. Both of these right-handed particles do not participate in the weak interaction, see (b) in Figure 08. The lepton number remains a conserved quantity in this case. But the predicted mass would be at least in the order of the electron's (too much) or the neutrino interactions with the Higgs boson at least 1012 times weaker than that of the top quark (too little) in an effort to reduce the mass.
- The Seesaw Mechanism - In this scheme, it is possible for right-handed neutrinos to have a mass of their own without relying on the Higgs boson. Unlike other quarks and leptons (including the electrons and left-handed neutrinos), the mass of the right-handed neutrino (a Dirac neutrino), M, is not tied to the mass scale of the Higgs boson, it can be much heavier than other particles. When a left-handed neutrino (a Majorana neutrino) collides with the Higgs boson (see (c) in Figure 08), it acquires a mass, m, which is comparable to the mass of other quarks and leptons. At the same time it transforms into a right-handed neutrino, which is much heavier than energy conservation would normally allow. This kind of virtual particle can occur in a very short time interval as ascribed by the uncertainty principle. The neutrino has an effective mass of m2/M from these two alternative states. For m ~ 100 Gev, and M ~ 1012 Gev, the neutrino mass would be of the order 1 ev. There is no need to reduce the strength for the Higgs coupling in this scenario. But the conservation of lepton number is violated. Such non-conserving process is still awaiting further experimental result (e.g., the neutrinoless double-beta-decay) to confirm. Although the seesaw model is extremely appealing in the sense that it gives a natural qualitative explanation of the smallness of neutrino masses, it still leaves too many possible reasonable combinations to use it for quantitative goals.
- The 5th Dimension - An alternative way exploits an idea from superstring theory in which the three dimensions of space are embedded in 10 or 11-dimensional space-time. It is proposed that all the particles of the Standard Model - electrons, quarks, left-handed neutrinos, the Higgs boson and so on - are stuck on a three-dimensional "sheet" called a three-brane. The 4th spatial dimension is "rolled up" on a circle with radius R (upper bound ~ 0.1 mm) such that it is not normally observable. There is another neutrino lives in the 4-dimensional bulk (the 4-D "volume") whose mass is of order 1/R (see Compactification). When this one mixes with the usual massless one, the net effect is to shift the mass by an order 1/R, which is identified with the observed neutrino mass.
- Neutrinos could constitute anything from 0.1 to 7 per cent of the mass of the universe (the dark matter). This range corresponds to the heaviest neutrino being in the mass range 0.05 to about 1 ev. Neutrinos any heavier than this would lead to galaxies being less clumped than actually observed by the recent 2dF Galaxy Redshift Survey.




 ( ij = 12, 13, 23) and the phase angle
( ij = 12, 13, 23) and the phase angle  are four parameters determining the amount of mixing and CP violation respectively, where
are four parameters determining the amount of mixing and CP violation respectively, where 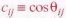 , and
, and 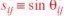 . The neutrino states on the left of the equation are the flavor states
. The neutrino states on the left of the equation are the flavor states
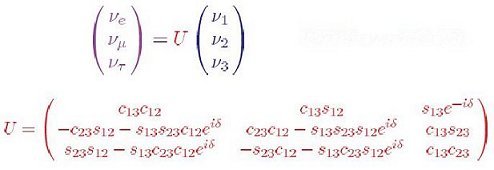



 and
and  ) is given by the relation:
) is given by the relation: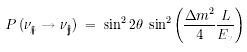
 =
=  ij is the mixing angle, L is the distance traveled by the neutrino, E stands for the energy of the neutrino, and
ij is the mixing angle, L is the distance traveled by the neutrino, E stands for the energy of the neutrino, and 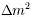 =
= 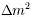 ij = mj2 - mi2 is the difference of the mass square. The mixing angles are determined from the amplitudes of the oscillation. The
ij = mj2 - mi2 is the difference of the mass square. The mixing angles are determined from the amplitudes of the oscillation. The 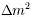 ijs can be calculated from the periods.
ijs can be calculated from the periods.
 12 ~ 30o, and
12 ~ 30o, and 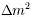 21 = 5x10-5 ev2.
21 = 5x10-5 ev2.  23 ~ 45o, and
23 ~ 45o, and 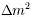 32 = 3.5x10-3 ev2.
32 = 3.5x10-3 ev2. 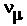 into
into 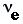 . It yields
. It yields 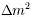 ~ 1 ev2 and
~ 1 ev2 and  ~ 0o, which is very different from the other measurements. A sterile neutrino is required to reconcile all the data as shown in Figure 07. Other experiments indicates
~ 0o, which is very different from the other measurements. A sterile neutrino is required to reconcile all the data as shown in Figure 07. Other experiments indicates  13 and the phase angle
13 and the phase angle  ~ 0o.
~ 0o.
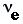 < 2.2 ev,
< 2.2 ev, 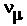 < 190 kev, and
< 190 kev, and 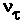 < 18.2 Mev.
< 18.2 Mev.
