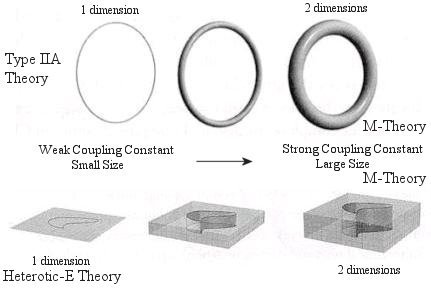
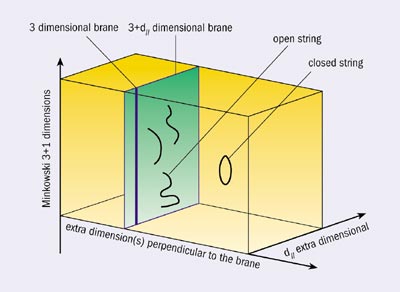
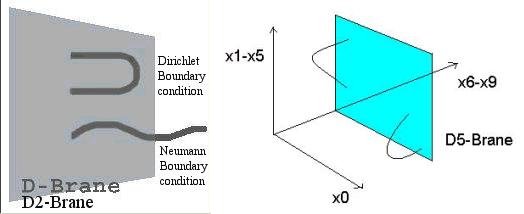
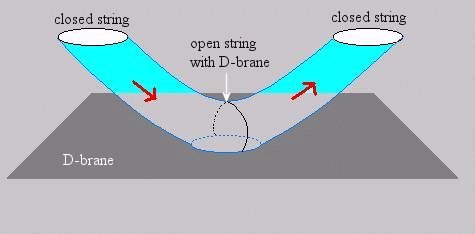
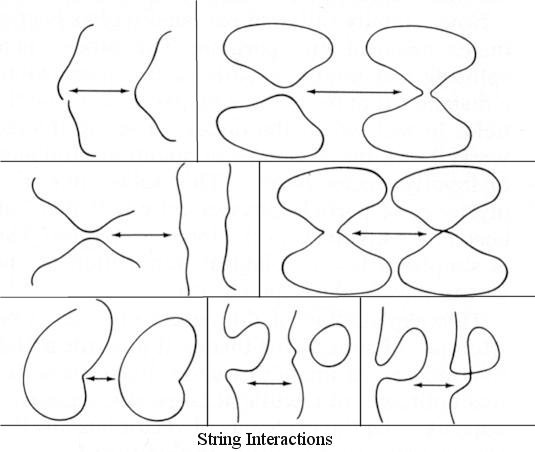
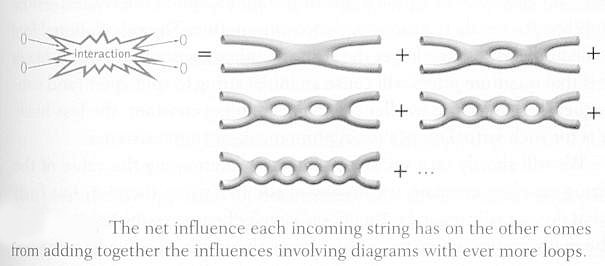
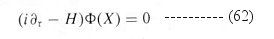 |
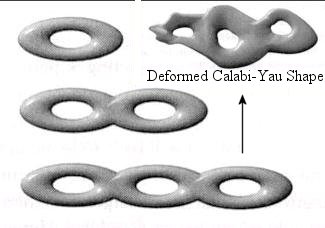
a family of lowest-energy string vibrations associated with each hole in the Calabi-Yau portion of space. Because the familiar elementary particles should correspond to the lowest-energy oscillatory patterns, the existence of multiple holes means that the patterns of string vibrations will fall into multiple families. If the curled-up Calabi-Yau has three holes, then we will find three families of elementary particles as observed. Unfortunately, the number of holes in each of the tens of thousands of known Calabi-Yau shapes spans a wide range from 3, 4, 5, 25, ... 480. |
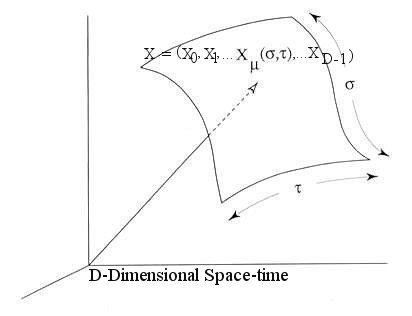
 (
(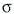 ,
,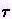 ) trace out a curve as
) trace out a curve as 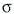 varies at fixed
varies at fixed 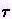 . The curve may be open or closed and
. The curve may be open or closed and 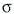 varies within a range between 0 and
varies within a range between 0 and 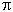 as the string is traced out from on end to the other for an open string, or once round the string for a closed string. The string sweeps out a world sheet as
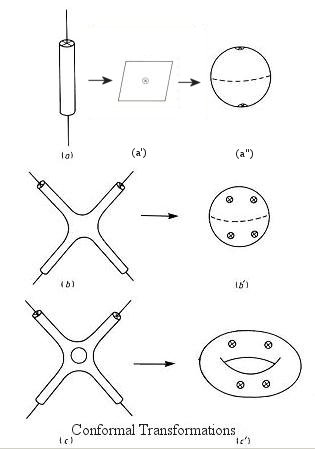
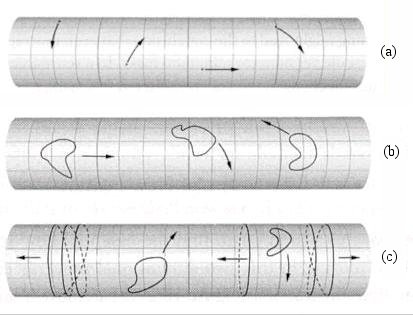
as the string is traced out from on end to the other for an open string, or once round the string for a closed string. The string sweeps out a world sheet as 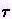 varies from one instant to another. However, these two parameters has nothing whatsoever to do with the real space and real time. Since nobody has ever seen or detected this artificial space-time, they have to be hidden from the obser- vables in a theory. Such theories are also said to be reparametrization invariant because they are not affected by the change to another set of artificial space-time parameters.
varies from one instant to another. However, these two parameters has nothing whatsoever to do with the real space and real time. Since nobody has ever seen or detected this artificial space-time, they have to be hidden from the obser- vables in a theory. Such theories are also said to be reparametrization invariant because they are not affected by the change to another set of artificial space-time parameters.
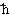 = 1, c = 1):
= 1, c = 1):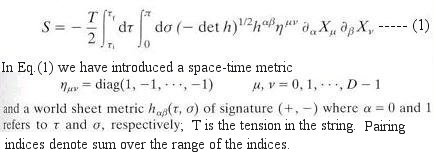
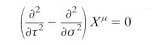
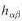 to minimize the action, more equations can be derived in the form:
to minimize the action, more equations can be derived in the form:
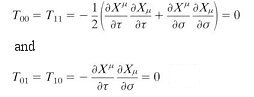
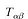 may be interpreted as the energy-momentum tensor for a two-dimensional field theory of "D" free scalar field X
may be interpreted as the energy-momentum tensor for a two-dimensional field theory of "D" free scalar field X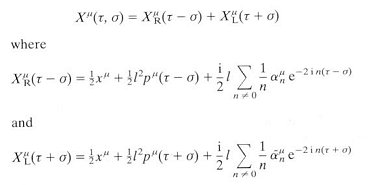
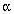 n
n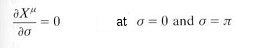
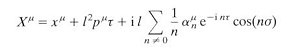
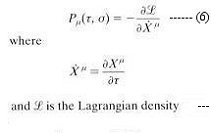

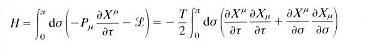
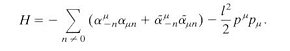
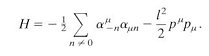
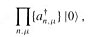
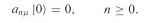 ---------- (20)
---------- (20)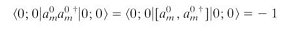
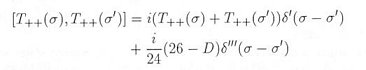

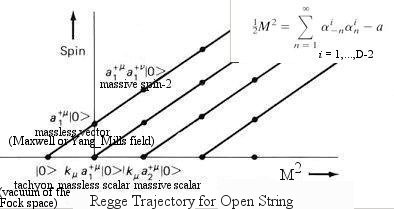
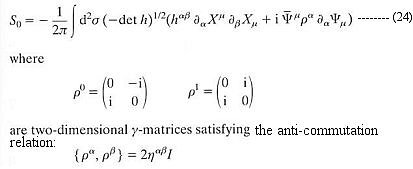
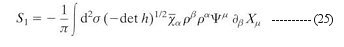
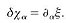 This cancellation scheme in turn gives another extra term, which is finally cancelled by S2 -
This cancellation scheme in turn gives another extra term, which is finally cancelled by S2 -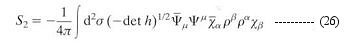
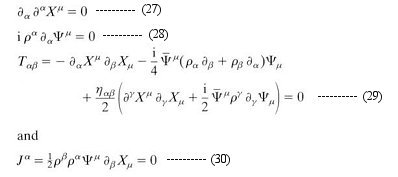
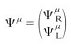
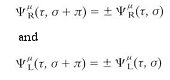
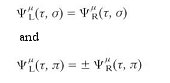
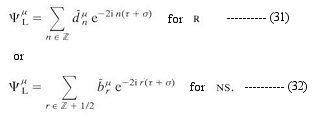
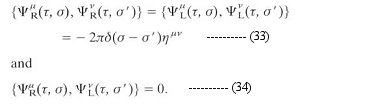
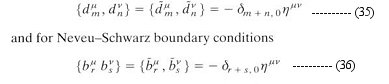
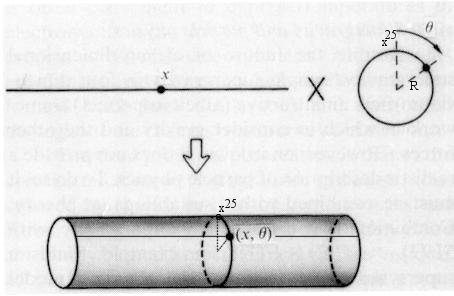
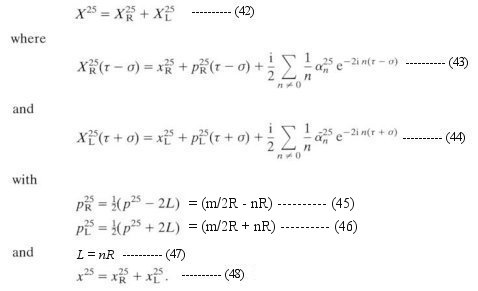
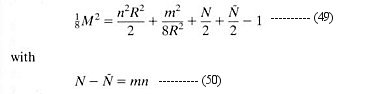
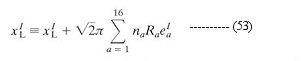
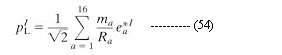
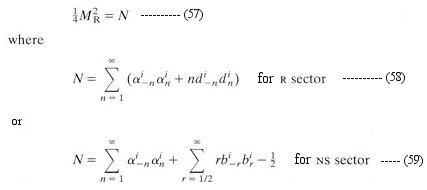
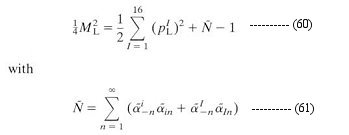
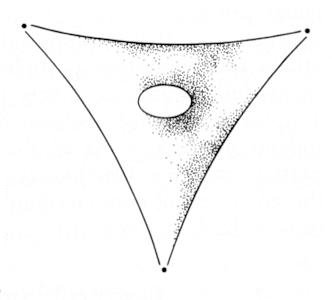


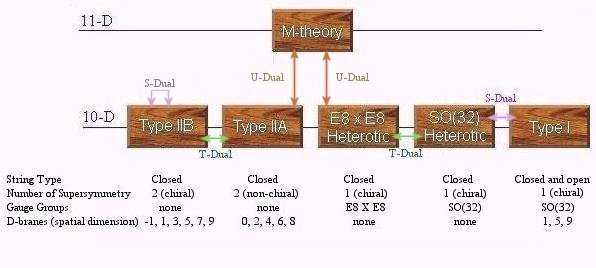
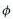 called dilaton. It can be shown that the Type IIB theory is invariant under a global transformation by the group SL(2,R) with the dilaton field transforming as
called dilaton. It can be shown that the Type IIB theory is invariant under a global transformation by the group SL(2,R) with the dilaton field transforming as