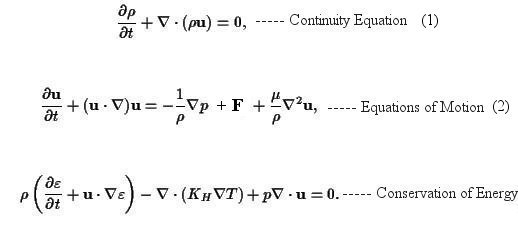
(3)
 x u = 0) are:
x u = 0) are:
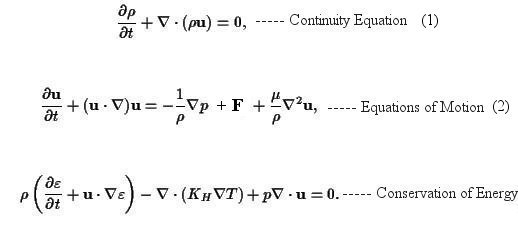 |
(3) |
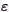 = thermodynamic internal energy, p = pressure, T = temperature,
= thermodynamic internal energy, p = pressure, T = temperature, 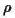 = density,
= density, 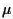 = viscosity, KH = heat conduction coefficient, and F = external force per unit mass.
= viscosity, KH = heat conduction coefficient, and F = external force per unit mass.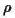 , temperature T, and three components of the velocity vector u. Together with the equation of state such as the ideal gas law - p V = n R T, the six equations are just enough to determine the six dependent variables. In general, all of the dependent variables are functions of all four independent variables. Usually, the Navier-Stokes equations are too complicated to be solved in a closed form. However, in some special cases the equations can be simplified and may admit analytical solutions.
, temperature T, and three components of the velocity vector u. Together with the equation of state such as the ideal gas law - p V = n R T, the six equations are just enough to determine the six dependent variables. In general, all of the dependent variables are functions of all four independent variables. Usually, the Navier-Stokes equations are too complicated to be solved in a closed form. However, in some special cases the equations can be simplified and may admit analytical solutions.
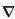
 u = 0. It is an idealization used to simplify analysis. In reality, all fluids are compressible to some extent.
u = 0. It is an idealization used to simplify analysis. In reality, all fluids are compressible to some extent. usL)/
usL)/ , where us is the mean fluid velocity, and L is the characteristic length, e.g., the cross-section of the pipe) can be used to evaluate whether viscous or inviscid equations are appropriate to the problem. High Reynolds numbers indicate that the inertial forces are more significant than the viscous forces. However, even in high Reynolds number regimes certain problems require that viscosity be included. In particular, problems calculating net forces on bodies (such as the wings on aircraft) should use viscous equations. Stokes flow occurs at very low Reynold's numbers, such that inertial forces can be neglected compared to viscous forces.
, where us is the mean fluid velocity, and L is the characteristic length, e.g., the cross-section of the pipe) can be used to evaluate whether viscous or inviscid equations are appropriate to the problem. High Reynolds numbers indicate that the inertial forces are more significant than the viscous forces. However, even in high Reynolds number regimes certain problems require that viscosity be included. In particular, problems calculating net forces on bodies (such as the wings on aircraft) should use viscous equations. Stokes flow occurs at very low Reynold's numbers, such that inertial forces can be neglected compared to viscous forces. 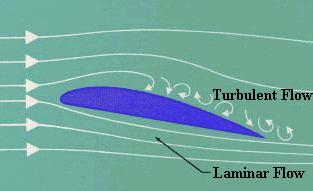 |
 |
instead modeled using one of a number of turbulence models and coupled with a flow solver that assumes laminar flow outside a turbulent region. Turbulence usually occurs below a Reynold's numbers of 3000. It causes increased energy loss (as heat), more drag (on the moving body), and generates sound wave (noise). |
Figure 01 Turbulent Flow [view large image] |
Figure 02 Laminar Flow [view large image] |
Modern vehicle and aircraft designs always try to minimize the turbulence by adopting a smooth surface and streamlined contour. |
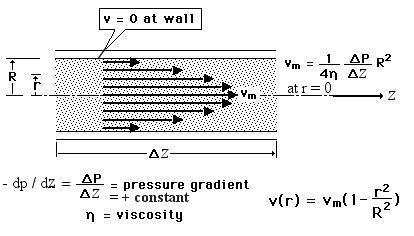
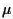 (1/r) d (r d v / dr) / dr ---------- (4)
(1/r) d (r d v / dr) / dr ---------- (4)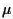 ) (- dp / dz) ---------- (6)
) (- dp / dz) ---------- (6)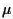 ~ infinity.
~ infinity.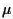 ) (- dp / dz) + v0 ---------- (7)
) (- dp / dz) + v0 ---------- (7) 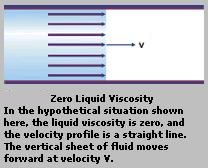 |
In case when the pressure gradient is absent, i.e., (- dp /dz) = 0 in Eqs.(4) and (7). The above solution is reduced to v(r) = vm = v0, that is, the flow has an uniform velocity similar to the case shown in Figure 03 for the uniform flow of inviscid fluid. But in this example, the viscosity term disappears in Eqs.(4) and (7) because (- dp /dz) = 0; and thus has no influence on the flow. It seems that the flow can last forever without a driving force. In reality, it would finally come to a halt by the dissipative effects and the discharge at the end of the pipe (in this example an infinitely long pipe is assumed). |
Figure 03 Uniform Flow [view large image] |
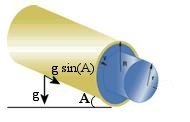 |
(- dp / dz) = 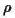 g sin(A) ---------- (9) g sin(A) ---------- (9)where 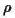 is the density of the fluid, g = 980 cm/sec2 is the acceleration of gravity, and is the density of the fluid, g = 980 cm/sec2 is the acceleration of gravity, and
|
Figure 04 Flow by Gravity Feed [view large image] |
sin(A) is related to the slant of the pipe. Such method is a convenient way to transport liquid, but it does not work for gas since its density is about 1000 times lower. |