Nuclei

Contents

Binding Energy

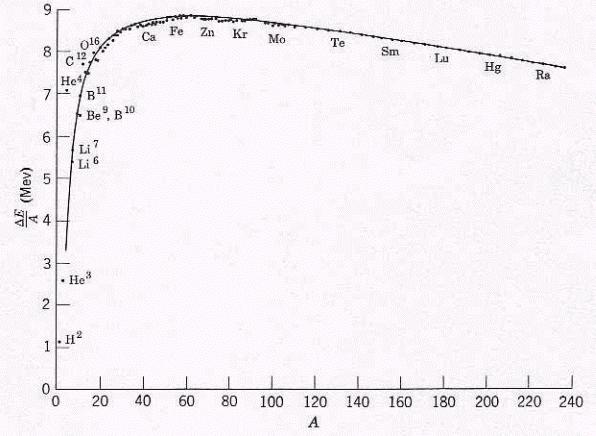
		A nucleus is specified by its number of protons Z, number of neutrons N, and the mass number A = Z+N. The nucleons (protons and neutrons) in a nucleus are bound together -- their total energy is less than the total energy of the separated particles. The binding energy is the amount of energy given up when the nucleus is formed. Plotting the binding energy per nucleon versus the mass number A (Figure 14-01) shows that starting from Hydrogen, nuclei become more
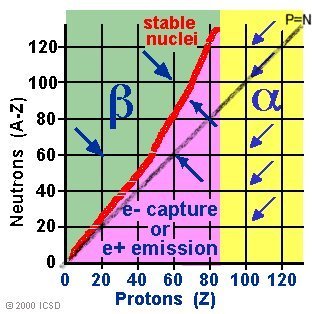
Figure 14-01 Nuclear Binding Energy [view large image]	Figure 14-02 Proton/Neutron & Decay [view large image]	stable as there are more protons and neutrons, until Iron. After that, the trend reverses.

Origin of Elements

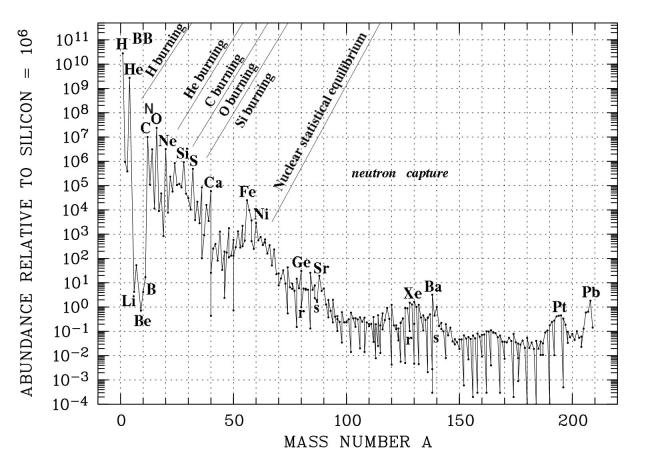Light elements (mainly hydrogen, helium and trace of deuterium, lithium) were generated in the first few minutes of the Big Bang, which was not able to produce more complex elements as the universe rapidly cooling off. Since then hydrogen and helium contribute by mass of respectively 70 and 28 per cent of all baryonic matter in the universe. Most of the remaining 2% of the elements up to iron and nickel are made in the interior of the stars. The resulting elements are thrust into space by booming stellar winds or when a star explodes as a supernova. Carbon, nitrogen and oxygen are the most abundant heavy elements. Oxygen is created by supernovae, while carbon is created in low-mass stars (red giants, planetary nebulae) and nitrogen is by a mixture of the above.

Figure 14-03 Element Abundance [view large

image]

The Liquid-Drop and The Shell Models

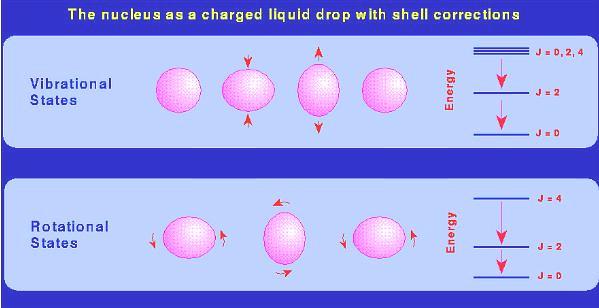
		The liquid-drop model assumes that the constituents of the nucleus interact only with their nearest neighbors, and the density is constant inside the nucleus, like the molecules in the liquid. Using this analogy, a semiempirical formula has been developed to describe the binding energy as a function of the mass number A (shown by the solid curve in Figure 14-01). The result is not particularly accurate for the lower value of A. The expression is useful in discussing stability, radioactivity, and the fluctuations from the average behavior due to shell effects. The top diagram in Figure 14-04a shows two vibrational energy levels, which split into finer structures due to rotation.
Figure 14-04a Liquid Drop Model [view large image]	Figure 14-04b Fission [view large image]	Figure 14-04b shows the deformation of the liquid drop, which eventually separates into two pieces (caused by the electrostatic repulsion of the protons).

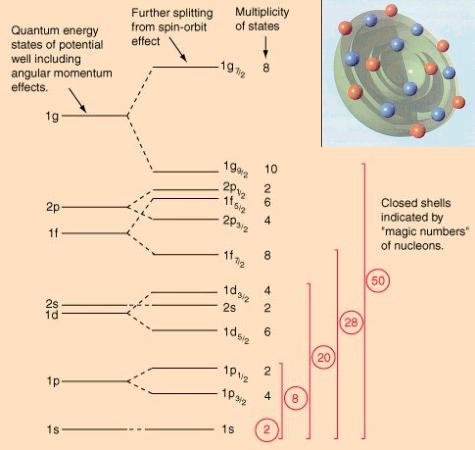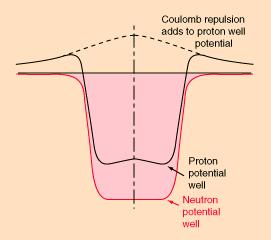
		There is extensive experimental evidence of the contrary hypothesis that the nucleons move in an effective potential well created by all the other nucleons. Since the nucleons are densely packed into a small region, it is expected that the chance of collision is very high. However, the interaction by collision is minimized by the Pauli exclusion principle, which forbids two fermions to occupy the same quantum state. If there are no nearby, unfilled quantum states that can be reached by the available energy for an interaction, then the interaction will not occur.
Figure 14-05a Nuclear Potential [view large image]	Figure 14-05b Nuclear Energy Levels [view large image]

• Enhanced abundance of those elements for which Z or N is a magic number.
• The stable elements at the end of the naturally occurring radioactive series all have a "magic number" of neutrons or protons.
• The neutron absorption cross-sections for isotopes where N = magic number are much lower than surrounding isotopes.
• The binding energy for the last neutron is a maximum for a magic neutron number and drops sharply for the next neutron added.
• Electric quadrupole moments (a measurement for deviation from spherical distribution) are near zero for magic number nuclei.
• The excitation energy from the ground nuclear state to the first excited state is greater for closed shells

Nuclear Decay

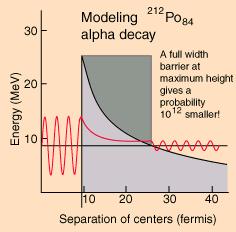
Unstable nuclei, called radioactive isotopes, will undergo nuclear decay to make it more stable. There are only certain types of nuclear decay which means that most isotopes can't jump directly from being unstable to being stable. It often takes several decays to eventually become a stable nucleus. When unstable nuclei decay, the reactions generally involve the emission of a particle and or energy. Half-lives are characteristic properties of the various unstable atomic nuclei and the particular way in which they decay. Alpha and beta decay are generally slower processes than gamma decay. Half-lives for beta decay range upward from 10^-2 sec and, for alpha decay, upward from about 10^-6 sec. Bismuth-209 has the longest half-life of 2x10¹⁹ years. Half-lives for gamma decay may be too short to measure (~ 10^-14 second), though a wide range of half-lives for gamma emission has been reported.

There are five types of nuclear decay:



Alpha Decay - The strong force, despite its strength, has a very short range; it can't even reach from one end of a fair-sized atomic nucleus to the other. If a proton is at the edge of a big nucleus, it can feel the pulling strong force only from the particles in the neighborhood, but there is an electromagnetic force, which tends to push it out, all the way from the other side of the nucleus. There is a sensitive balance between these two competing forces. The nucleus needs not to acquire extra energy to escape; the quantum mechanical effect called tunneling allows a certain probability of escape through a potential wall. Alpha decay, in which just a small chunk breaks off from the main nucleus, is a rather mild case of fission; in more dramatic examples, the nucleus can break more or less in half. The broken-off chunk most often is packed into a helium nucleus (alpha particle) because it is in a more stable form. Figure 14-06 shows the effect of tunneling

Figure 14-06 Alpha Decay [view large image]

through the Coulomb barrier; the nucleus has a small probability of escape to the outside depending on the height and width of the wall.

Beta Decay - The weak interaction is responsible for the instability of "free" neutrons, which decay according to the reaction: n ==> p + e + electron-anti-neutrino with a lifetime about 15 minutes in a process known as beta decay. Neutrons in a nucleus are subject to the protection of the nuclear and the electromagnetic forces from the other nucleons, and they will remain stable provided there are not too many of them. If there are too many, such protection would not be sufficient for all of them to remain stable, and the nucleus would undergo beta decay. Figure 14-07

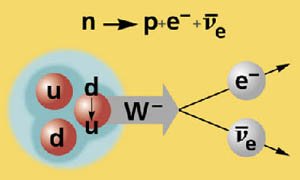
Figure 14-07 Beta Decay [view large image]

shows that in the beta decay process, the down quark turns into an up quark (thus changes the neutron to proton) by emitting a W- meson, which decays into an electron and an electron-anti-neutrino.

Gamma Decay - In gamma decay, a nucleus changes from a higher energy state to a lower energy state through the emission of electromagnetic radiation. It happens usually after the transmutation of the nucleus; the end product has to re-arrange the occupancy of energy levels in order to arrive at a more stable state. The number of protons (and neutrons) in the nucleus does not change in this process, so the parent and daughter atoms are the same chemical element. In the gamma decay of a nucleus, the emitted photon and recoiling nucleus each have a well-defined energy after the decay. Figure 14-08 shows the adjustment of energy level by emitting gamma ray after Mg has transmuted into Al.

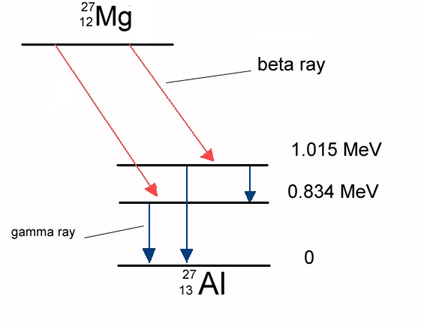
Figure 14-08 Gamma Decay [view large image]

• Positron Emission - Positron emission is a type of beta decay, referred to as "beta plus"(ß+ ) or inverse beta decay. In beta plus decay, a proton is converted to a neutron, a positron and a neutrino via the weak interaction. This spontaneous nuclear process releases an amount of energy equal to the energy equivalent of the rest mass that disappears in the process. The positron and neutrino are created in the nucleus at the moment of disintegration. The "endothermic reactions" receives the energy from the nuclear fission. That positron decay is a nuclear process is consistent with the fact that the decay of free protons by positron emission is not observed in nature. On the other hand, the beta decay of free neutrons is a familiar fact. The positron is made of anti-matter and does not last very long in the world of ordinary matter. As soon as the positron meets an ordinary electron the two particles annihilate and

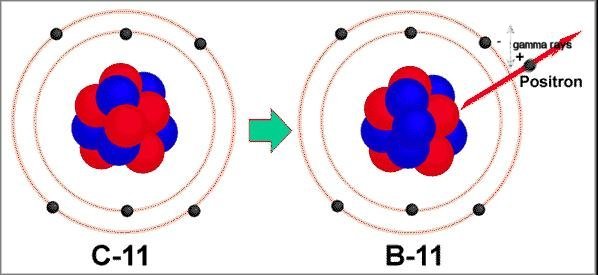the energy contained in their mass appears as two gamma-rays of 0.5 MeV each, flying off in opposite directions. Positron radioactivity is therefore always accompanied by the emission of gamma rays with an energy of about 0.5 MeV in addition to any other gamma-rays which might be emitted. Example isotopes, which emit positrons are C-11, N-13, O-15 and F-18. These isotopes are used in positron emission tomography (PET). Figure 14-09 shows the transmutation of C-11 into B-11 by positron emission.

Figure 14-09 Positron Emission [view large image]

• Electron Capture - Electron capture is a decay mode for nucleus that will occur when there are too many protons in the nucleus of an atom, and there isn't enough energy to emit a positron. In this case, one of the orbital electrons is captured by a proton in the nucleus, forming a neutron and a neutrino. Since the proton is essentially changed to a neutron, the

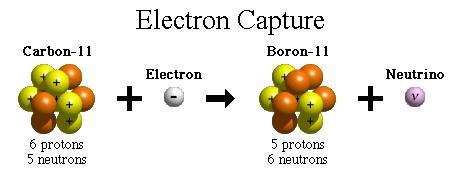	number of neutrons increases by 1, the number of protons decreases by 1, and the atomic mass remains unchanged. By changing the number of protons, electron capture transforms the nucleus into a new element. Electron capture is also called K-capture since the captured electron usually comes from the atom's K-shell. Figure 14-10 shows another way of transmuting C-11 into B-11 by electron capture.
Figure 14-10 Electron Capture [view large image]

Table 14-01 Types of Nuclear Decay

Fission

		If a massive nucleus like uranium-235 breaks apart (fission), then there will be a net yield of energy because the sum of the masses of the fragments will be less than the mass of the uranium nucleus. If the mass of the fragments is equal to or greater than that of iron at the peak of the binding energy curve,
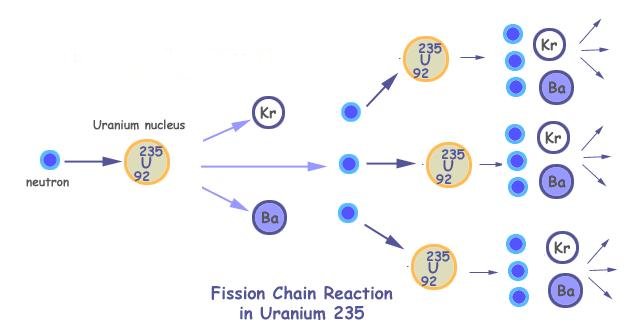
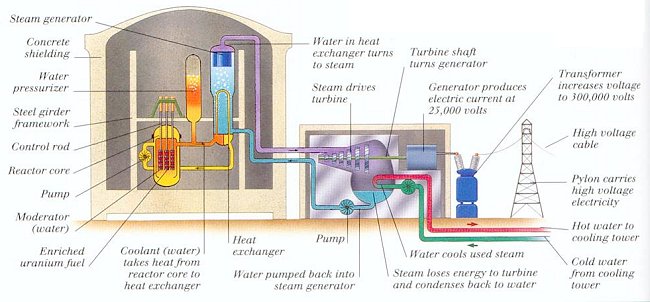
Figure 14-11 Chain Reaction [view large image]	Figure 14-12 Nuclear Reactor [view large image]	(see Figure 14-01) then the products of the decay will be more tightly bound than they were in the uranium nucleus, and that decrease in mass comes off

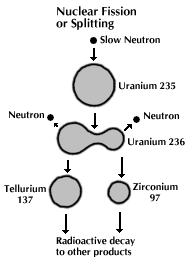
In one of the most remarkable phenomena in nature, a neutron can be captured by a uranium-235 nucleus, rendering it unstable toward nuclear fission. When a U-235 nucleus splits, it gives off energy in the form of heat and Gamma radiation, which is the most powerful form of radioactivity and the most lethal. When this reaction occurs, the split nucleus will also give off two or three of its `spare' neutrons. These spare neutrons fly out to split other U-235 nuclei they come in contact with. In theory, it is necessary to split only one U-235 nucleus, and the neutrons from this will split other U-235 nuclei, which will split more...so on and so forth -- a chain reaction. (See Figure 14-11.) This progression does not take place arithmetically, but geometrically. All of this will happen within a millionth of a second. The minimum amount to start a chain reaction as described above is known as Critical Mass. The actual mass needed to facilitate this chain reaction depends upon the purity of the material and whether it is tampered. The tamper is a thick casing made of natural uranium. It reflected neutrons back into the core and helped to hold it together for a fraction of a second. For pure U-235, the bare critical mass is 50 kg and the tampered critical mass is 15 kg (with a spherical tamper size of 11.5 cm diameter); it is 10 kg and 5 kg respectively for Pu-239 (with 8 cm tamper size).

Table 14-02 Fissionable Isotopes

Fusion

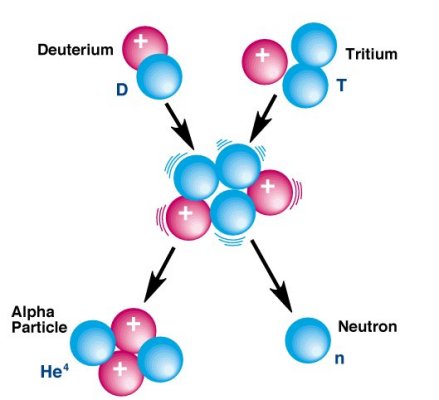
		Thermonuclear, or hydrogen bombs explode with enormous power via uncontrolled self-sustaining chain fusion reactions. Deuterium and tritium form helium under extremely high temperature, providing the energy: D + T ==> He + n + 17.6 Mev (See Figure 14-13.) In principle, a mixture of D and T heated to very high temperature and in high density will start a chain fusion
Figure 14-13 Fusion [view large image]	Figure 14-14 Thermalnuclear Explosion [view large image]	reaction, liberating an enormous amount of energy. But tritium is an unstable element; an ingenious method is to have it produced from lithium deuterate (Li6H2) in

Effects of Nuclear Explosions

Effects of the blast include (see Figure 14-15 for the effects on Hiroshima):


• A wave of intense heat from the explosion.
• Pressure from the shock wave created by the blast.
• Radiation.
• Radioactive fallout (clouds of fine radioactive particles of dust and bomb debris that fall back to the ground).

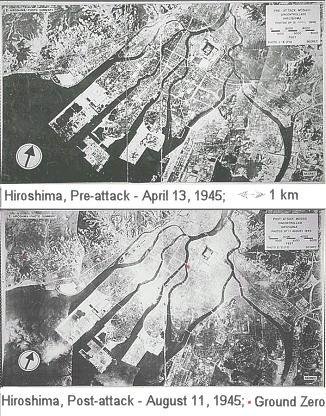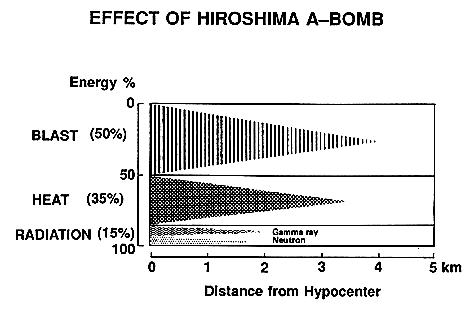
		At the hypocenter (ground zero), everything is immediately vaporized by the high temperature (up to 300 million oC). Outward from the hypocenter, most casualties are caused by burns from the heat, injuries from the flying debris of buildings collapsed by the shock wave, and acute exposure to the high radiation. Beyond the immediate blast area, casualties are caused from the heat, radiation, and fires spawned from the heat wave. Figure 14-16 presents two views of Hiroshima before and after an atomic-bomb attack. It occurred in the morning (8:16 a.m.) of August 6, 1945.
Figure 14-15 Effects of A-Bomb [view large image]	Figure 14-16 Hiroshima [view large image]	The bomb detonated at an altitude of 580 meters killing or wounding about half of its 350,000 inhabitants with long-term effects on incalculable numbers among the survivors.

Some of the resulting health conditions include:


• Nausea, vomiting and diarrhea.
• Cataracts.
• Hair loss.
• Loss of blood cells.
• Infertility.
• Birth defects.
• Leukemia.
• Cancer.

References:

• Binding Energy -- http://hyperphysics.phy-astr.gsu.edu/hbase/nucene/nucbin.html
• Nuclear Models -- http://csep1.phy.ornl.gov/guidry/Math-9-94html/models.html
• Nuclear Decay, Fission, Fusion -- http://www.lbl.gov/abc/Basic.html
• Nuclear Energy -- http://zebu.uoregon.edu/1999/ph161/l18.html
• Nuclear Reactor -- http://www.npp.hu/mukodes/lancreakcio-e.htm
• Hiroshima, Effect of A-Bomb -- http://www.pref.hiroshima.jp/hiroshima/bunka/htmleng/elegacy3.htm

[Top]

---

Index

Alpha decay Beta decay Binding energy Cobalt bomb Critical mass Doomsday machine Electron capture Fission Fusion Gamma decay Liquid drop model

Magic number Mass number Multiplicity Neutron bomb Nuclear decay Plutonium 239 Positron emission Radioactive series Shell model Uranium 235

---

[Home Page]