Following is a very simple differential equation applicable to exponential decay such as the decay of radioactive element. In plain language, it states that the decrement of y (hence the minus sign) over a small time interval depends on the amount y. The parameter k is a proportional constant which is called the rate of decay in this case, and is unique to a particular system. For example, if k = 0, then y is not decaying at all. Thus
dy/dt = -k y -------------------------------- (1)
where dy = y(t2) - y(t1) is an infinitesimal change of the function y in an infinitesimal time interval dt = t2 - t1 with t2 > t1.
It can be shown by direct subsitution (and with the rule of calculus) that the solution of Eq.(1) is
y = A e-kt
where e=2.71828 is the expnential base used in calculus to simplify the form of many formulas, and A is an arbitarry constant to be determined by the initial condition. For example, if at t = 0, y = yo, then A = yo.
The final solution is:
y = yo e-kt --------------------------------- (2)
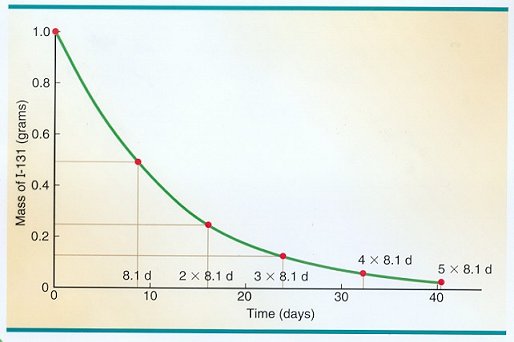
The following is a curve for the radioactive decay of Iodine 131 with a half life of 8.1 days. Half life is the interval when half of the original is gone. This graph corresponds to 1/k = 8.1/loge(2) = 11.57 d., and yo = 1 gm. in Eq.(2).