 |
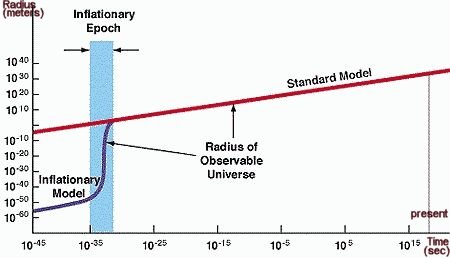
According to the latest cosmological model, the universe sprang into being about 14 billion years ago. At birth, the space was likely to have been curved and warped due to quantum effect within the tiny speck and time may be meaningless. After about 10-35 seconds, there began a brief period of exponentially fast expansion, known as inflation, that ironed out any curves or warps in space and made the universe flat (because it becomes so large). Inflation also predicts a much smaller initial region, which is required for smoothing out the distribution of matter and radiation, only leaving behind tiny density fluc- |
Figure 01 Cosmic Inflation |
tuations that match the observed spatial variations in the cosmic microwave background radiation and provide the seeds for galaxy formation. |
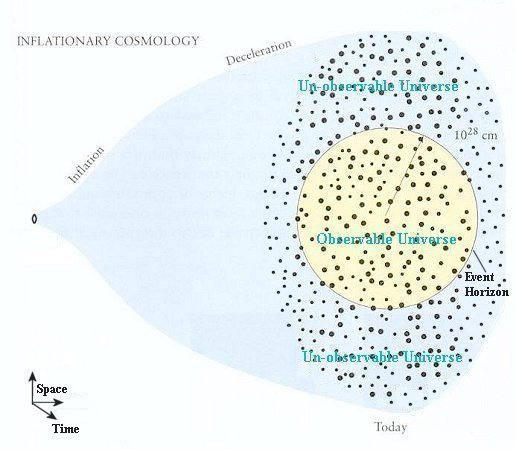 |
The blue strip in Figure 01 shows the period of inflation from 10-35 sec to 10-32 sec after the initial expansion. Figure 02 shows the actual size of the universe after the inflation. Our observable unvierse is only part of the whole thing. The mechanism to drive the inflation is related to a "yet-to-be-discovered" inflaton field, which is thought to be similar to the Higgs fields responsible for the mass of the elementary particles. When the temperature fell below a certain value, a phase transition (similar to the transition of water to ice at 0oC with the release of latent heat) of the inflaton field occurred. The phase transition released energy, which was conversed to hot matter and radiation. It also developed repulsive force to drive the inflation. The inflation stopped when the inflaton field settled down into lower energy state. |
Figure 02 Unobservable Universe |
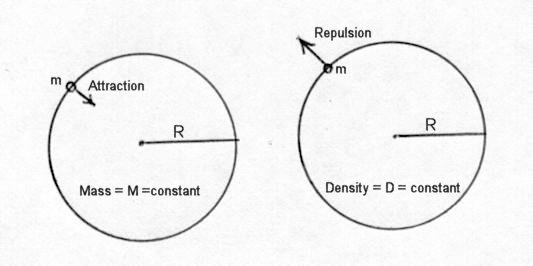 |
The concept of cosmic inflation can be illustrated by simple mathematics using only elementary calculus. Suppose the universe is uniform and isotropic as demonstrated by observations. This means that every point in the universe is similar to every other point and can be considered as the "centre" (Figure 03). Now consider a "test particle" of mass m and at distance R from the centre. Since only mass inside the sphere has a net effect on the particle, and if the total mass M insider the sphere of radius R is constant, then the potential energy of |
Figure 03 Repulsion vs Attraction |
the particle is: |
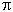 /3) x R2 ---------- (3)
/3) x R2 ---------- (3) 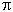 /3) x R ---------- (4)
/3) x R ---------- (4) /3) x D x R3 ---------- (5)
/3) x D x R3 ---------- (5)  |
Figure 04 shows the variation of the energy density since the Big Bang. It maintained a constant value during the inflationary era as described in the simple mathematical model. The energy density of water (1021 ergs/cm3) and of an atomic nucleus (1036 ergs/cm3) are included in the graph for comparison.
[view large image] |
Figure 04 Energy Density |