The ALU is that part of the computer that actually performs arithmetic and logical operations on data. All of the other elements of the computer system—control unit, registers, memory, I/O—are there mainly to bring data into the ALU for it to process and then to take the results back out. 
An ALU and, indeed, all electronic components in the computer arc based on the use of simple digital logic devices that can store binary digits and perform simple Boolean logic operations.
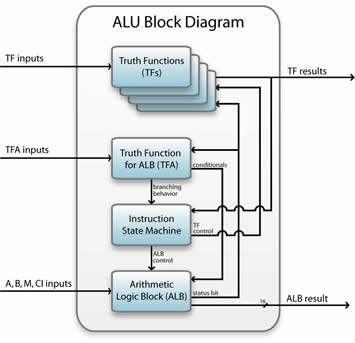
ALU is interconnected with the rest of the processor. Data are presented to the ALU in registers, and the results of an operation are stored in registers. These registers are temporary storage locations within the processor that are connected by signal paths to the ALU. The ALU may also set flags as the result of an operation.
For example, an overflow flag is set to 1 if the result of a computation exceeds the length of the register into which it is to be stored.
Integer Representation
In the binary number system, arbitrary numbers can be represented with just the digits zero and one, the minus sign, and the period, or radix point.
however, we do not have the benefit of minus signs and periods. Only binary digits (0 and 1) may be used lo represent numbers.
Unsigned/Signed Integer
There are several alternative conventions used to represent negative as well as positive integers, all of which involve treating the most significant (leftmost) bit in the word as a sign bit.
If the sign bit is 0, the number is positive: if the sign bit is 1, the number is negative.
For example: +18= 0 0010010
- 18=1 0010010
There are several drawbacks to sign-magnitude representation. One is that addition and subtraction require a consideration of both the signs of the numbers and their relative magnitudes to carry out the required operation.
Another drawback is that there are two representations of 0 (e.g 0000 0000 and 1000 00000).
This is inconvenient, because it is slightly more difficult to test for 0 (an operation performed frequently on computers) than if there were a single representation.
Because of these drawbacks, sign-magnitude representation is rarely used in implementing the integer portion of the ALU. Instead, the most common scheme is twos complement representation.
Ones Complement
The ones complement of a number is represented by flipping the number's bits one at a time. For example, the value 01001001 becomes 10110110.
Twos complement
There is a simple way to calculate a twos complement value: invert the number's bits and then add 1.
For an example:
consider the value 17 which is 00010001 in binary. Inverting gives 11101110. Adding one makes this 11101111.
Twos Complement Representation
Like sign magnitude, twos complement representation uses the most significant bit as a sign bit, making it easy to test whether an integer is positive or negative.
Converting between Different Bit Lengths
The rule for twos complement integers is to move the sign hit to the new leftmost position and fill in with copies of the sign bit. For positive numbers, fill in with zeros, and for negative numbers, till in with ones.
For example:
+18 = 00010010
+18 = 00000000 00010010
-18 = 10010010
-18 = 11111111 10010010
 ශිල්ප 64
ශිල්ප 64