සෘඡුකෝණී ත්රිකෝණයක පාදවල දිග අතර පවතින අනුපාතයන්
සයින,කෝසයින හා ටැංඡන ලෙස හඳුන්වන අතර ඒවා කෙටියෙන් සයින්,කොස් හා ටෑන් ලෙසද හඳුන්වයි.
සයින,කෝසයින හා ටැංඡන ලෙස හඳුන්වන අතර ඒවා කෙටියෙන් සයින්,කොස් හා ටෑන් ලෙසද හඳුන්වයි.
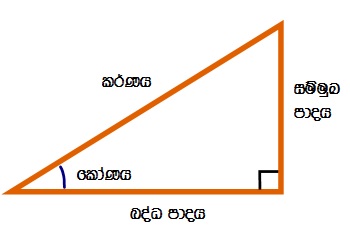
අර්ථ දක්වා ඇති පරිදි
සයින්= සම්මුඛ පාදය / කර්ණය වේ
කොස්= බද්ධ පාදය / කර්ණය වේ
ටෑන්= සම්මුඛ පාදය/ බද්ධ පාදය වේ
කර්ණය යනු සෘජු කොණී ත්රිකෝණයක දිගම පාදය බැවින්
සයින්= සම්මුඛ පාදය / කර්ණය වේ
කොස්= බද්ධ පාදය / කර්ණය වේ
ටෑන්= සම්මුඛ පාදය/ බද්ධ පාදය වේ
කර්ණය යනු සෘජු කොණී ත්රිකෝණයක දිගම පාදය බැවින්
සයින් හා කොස් නිතරම 1ට අඩු අගයක් ගනී.
ටෑන් තීරණය වන්නේ බද්ධ පාදය හා සම්මුඛ පාදය අනුව බැවින් එම අගය 1ට අඩු හෝ වැඩි විය හැක. මේ කිසිම අගයක් සෘණ විය නොහැක.
ටෑන් තීරණය වන්නේ බද්ධ පාදය හා සම්මුඛ පාදය අනුව බැවින් එම අගය 1ට අඩු හෝ වැඩි විය හැක. මේ කිසිම අගයක් සෘණ විය නොහැක.
මේවා වැදගත් වන්නේ ඇයි?
ඔබ කිසියම් සෘඡුකෝණී ත්රිකෝණයක එක් කෝණයක් හා ඉහත අනුපාතයක් දන්නේ යැයි සිතමු.
එවිට ඔබට එහි ඉතිරි පාදය පහසුවෙන් සොයාගත හැකිවනු ඇත.
ඔබ කිසියම් ස්ථානයක සිට ඔබට දුරින් වන කන්දක් පාමුලට ඇති දුර හා එම කන්ද මුදුන ඔබට පෙනෙන ආරෝහණ කෝණය දන්නේ නම් ඉහත අනුපාතයන් මඟින් එම කන්දේ උස පහසුවෙන් ගණනය කලහැක.
ටෑන් සලකා බලමු.
පහතින් සෘඡුකෝණයක් දක්වා ඇති අතර එහි ඉතිරි කෝණයක් 45 බවද දී ඇත.
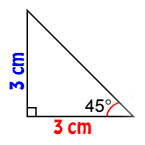
අර්ථ දැක්වීම අනුව,
ටෑන් 45= සම්මුඛ පාදය/බද්ධ පාදය
= 3 ÷ 3
ටෑන් 45 = 1
සෘඡුකෝණී ත්රිකෝණ සඳහා සෑමවිටම ටෑන් 45 = 1වේ.
= 3 ÷ 3
ටෑන් 45 = 1
සෘඡුකෝණී ත්රිකෝණ සඳහා සෑමවිටම ටෑන් 45 = 1වේ.
අප දැන් නොදන්නා A නම් කෝණයක් සඳහා ටෑන් සලකා බලමු.
අර්ථ දැක්වීම අනුව, ටෑන් 45= සම්මුඛ පාදය:බද්ධ පාදය
ටෑන් A = 1÷4 = 0.25
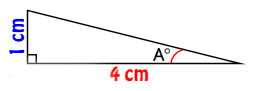
නමුත් මෙහිදී A නම් කෝණයෙහි අගය කීයද? ටෑන් 14 = 0.25
කොස්
අප පහත දැක්වෙන සෘඡුකෝණී ත්රිකෝණය සලකා බලමු.
එහි පාද 2ක් හා 60ක් ලෙස කෝණයක්ද දක්වා ඇත.
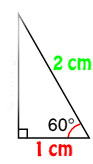
අර්ථ දැක්වීම අනුව,
කොස් = බද්ධ පාදය:කර්ණය
කොස් 60 =1÷2
=0.5
සෘඡුකෝණී ත්රිකෝණ සඳහා සෑමවිටම කොස් 60 =0.5 වේ.
සයින්
සෘඡුකෝණී ත්රිකෝණය පාද 2ක් හා අංශක 30ක කෝණයක්ද දක්වා ඇත.
අර්ථ දැක්වීම අනුව, සයින් = සම්මුඛ පාදය/කර්ණය
සයින් 30 = 4 ÷8
සයින් 30 = 0.5
මේ අනුව, සෘඡුකෝණී ත්රිකෝණ සඳහා සෑමවිටම සයින් 30 = 0.5 වේ.
ප්රතිසයින.
මෙහිදී සෘඡුකෝණී ත්රිකෝණයක සලකනු ලබන යම් කෝණයක,
සම්මුඛ පාදය:කර්ණය යන අනුපාතය හෙවත් එම කෝණයේ සයින් අගය දන්නාවිට එම කෝණය සොයාගත හැක.
අර්ථ දැක්වීම අනුව, සයින් = සම්මුඛ පාදය:කර්ණය
සයින් v = 3 ÷ 3.6
සයින් v = 0.833
දැන් අපට සයින් වගුවක් ආධාරයෙන් v හි අගය ගණනය කරගත හැක.
සෘඡුකෝණී ත්රිකෝණය පාද 2ක් හා අංශක 30ක කෝණයක්ද දක්වා ඇත.
අර්ථ දැක්වීම අනුව, සයින් = සම්මුඛ පාදය/කර්ණය
සයින් 30 = 4 ÷8
සයින් 30 = 0.5
මේ අනුව, සෘඡුකෝණී ත්රිකෝණ සඳහා සෑමවිටම සයින් 30 = 0.5 වේ.
ප්රතිසයින.
මෙහිදී සෘඡුකෝණී ත්රිකෝණයක සලකනු ලබන යම් කෝණයක,
සම්මුඛ පාදය:කර්ණය යන අනුපාතය හෙවත් එම කෝණයේ සයින් අගය දන්නාවිට එම කෝණය සොයාගත හැක.
අර්ථ දැක්වීම අනුව, සයින් = සම්මුඛ පාදය:කර්ණය
සයින් v = 3 ÷ 3.6
සයින් v = 0.833
දැන් අපට සයින් වගුවක් ආධාරයෙන් v හි අගය ගණනය කරගත හැක.
ප්රති-කොස් හා ටෑන්
ඉහත නොදන්නා කෝණයක සයින් අගය දන්නා විට ප්රතිසයින් මඟින් එම කෝණය සොයා ගත් ආකාරයටම කිසියම් කෝණයක කොස් හෝ ටෑන් අගය දන්නේ නම් එවිටද ප්රතිටෑන් හෝ කොස් මඟින් එම නොදන්නා කෝණය සොයාගතහැක.
අර්ථ දැක්වීම අනුව,
කොස් = බද්ධ පාදය:කර්ණය
කොස් v = 2 ÷ 3.6
කොස් v= 0.556
දැන් අපට සයින් හෝ ටෑන් වගුවක් ආධාරයෙන් v හි අගය ගණනය කරගත හැක.
 ශිල්ප 64
ශිල්ප 64