ත්රිකෝණමිතිය ඈත අතීතයේ සිට පැවත එන මිනුම් ක්රමයකි.
ආදී ග්රීකයන් විසින් මෙමඟින් සූර්යයා,තාරකා ආදිය නිරීක්ෂණයට යොදා ගත්හ.
ත්රිකෝණමිතියේ භාවිතා බොහොමයක් හමුවන්නේ ආදී ඊජිප්තුවෙනි.
ඔබ පිරමිඩවල පින්තූර දැක තිබේද ?


ත්රිකෝණයක් සැලකූවිට එහි එක් කෝණයක් අංශක 90 ක් වේ නම් එය ඍඡුකෝණී ත්රිකෝණයක් වන අතර ,එම කෝණයට ඉදිරියෙන් ඇති පාදය කර්ණය නම් වේ.
ආදී ග්රීකයන් විසින් මෙමඟින් සූර්යයා,තාරකා ආදිය නිරීක්ෂණයට යොදා ගත්හ.
ත්රිකෝණමිතියේ භාවිතා බොහොමයක් හමුවන්නේ ආදී ඊජිප්තුවෙනි.
ඔබ පිරමිඩවල පින්තූර දැක තිබේද ?


ත්රිකෝණයක් සැලකූවිට එහි එක් කෝණයක් අංශක 90 ක් වේ නම් එය ඍඡුකෝණී ත්රිකෝණයක් වන අතර ,එම කෝණයට ඉදිරියෙන් ඇති පාදය කර්ණය නම් වේ.
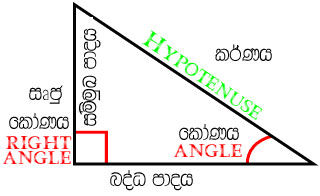
ඍඡුකෝණී ත්රිකෝණයක පාද හඳුනාගනිමු.
ඍඡුකෝණයක ඉදිරියේ ඇති පාදය එනම් ඍඡුකෝණී ත්රිකෝණයක දිගම පාදය කර්ණයද, ඉතිරි කෝණ දෙකෙන් එක් කෝණයක් සැලකූවිට එය ඉදිරියේ ඇති පාදය සම්මුඛ පාදය ලෙසද
එම කෝණයට යාබද පාදය බද්ධ පාදය ලෙසද හඳුන්වයි.
එම කෝණයට යාබද පාදය බද්ධ පාදය ලෙසද හඳුන්වයි.
පයිතගරස් ප්රමේයය.
ක්රි:පූ 580-500 අතර කාලයේ විසූ ග්රීක දාර්ශනිකයෙකු හා ශ්රේෂ්ඨ ගණිතඥයකු වූ පයිතගරස් විසින් ඍඡුකෝණී ත්රිකෝණයක පාදවල දුර අතර සම්බන්ධයක් පෙන්වා දෙන ලදී.
ක්රි:පූ 580-500 අතර කාලයේ විසූ ග්රීක දාර්ශනිකයෙකු හා ශ්රේෂ්ඨ ගණිතඥයකු වූ පයිතගරස් විසින් ඍඡුකෝණී ත්රිකෝණයක පාදවල දුර අතර සම්බන්ධයක් පෙන්වා දෙන ලදී.
කර්ණය2=සම්මුඛ පාදය2 + බද්ධ පාදය2
මෙය පයිතගරස් ප්රමේයය නම් වන අතර එය සෑම ඍඡුකෝණී ත්රිකෝණයකටම වලංගුවේ.
පාද අතර අනුපාත.
කෝණ සමාන නමුත් පාද වල දිග වෙනස් ත්රිකෝණ සමරූපී ත්රිකෝණ වන අතර සමරූපීතාවය පෙන්වන සෘඡුකෝණී ත්රිකෝණවල පාද අතර ඇත්තේ එකම අනුපාතයකි.
කෝණ සමාන නමුත් පාද වල දිග වෙනස් ත්රිකෝණ සමරූපී ත්රිකෝණ වන අතර සමරූපීතාවය පෙන්වන සෘඡුකෝණී ත්රිකෝණවල පාද අතර ඇත්තේ එකම අනුපාතයකි.
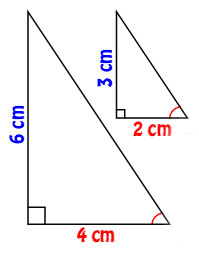
ඉහත දැක්වෙන ත්රිකෝණ දෙක සමරූපී වේ.
එහි විශාල ත්රිකෝණයේ පාද කුඩා ත්රිකෝණයේ පාද මෙන් හරියටම දෙගුණයක් වෙයි.
නමුත් ඒවායේ කෝණ වල කිසිඳු වෙනසක් නැත.
ඉහත සමරූපී ත්රිකෝණ දෙකෙහිම සම්මුඛ පාදය:බද්ධ පාදය යන අනුපාතය 3:2 වේ.
සෘඡුකෝණී ත්රිකෝණවල පාදවල දිග අතර අනුපාතය ඉතා වැදගත්වේ.
පාද අතර අනුපාතය ත්රිකෝණයේ කෝණ වල ප්රමාණයට බලපායි.
 ශිල්ප 64
ශිල්ප 64