DeMorgan's theorems are extremely useful in simplifying expressions in which a product or sum of variables is inverted.
The two theorems are:
The two theorems are:
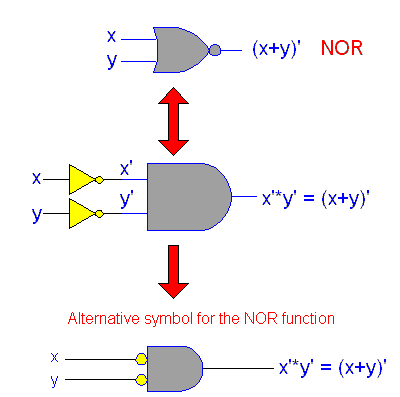
1. (x+y)' = x' * y'
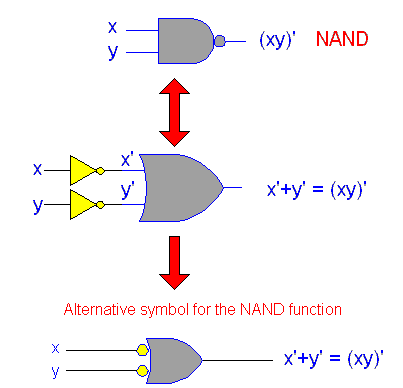
2. (x*y)' = x' + y'
Theorem 1 says that when the OR sum of two variables is inverted, this is the same as inverting each variable individually and then ANDing these inverted variables.
Theorem 2 says that when the AND product of two variables is inverted, this is the same as inverting each variable individually and then ORing them.
X = [(A'+C) * (B+D')]'
= (A'+C)' + (B+D')' [by theorem 1 ]
= (A''*C') + (B'+D'') [by theorem 2]
= AC' + B'D
Using Truth Tables
(A+B) = A.B
| = |
|
(A.B) = A+B
| = |
|
Three Variables DeMorgan's Theorem
3. (x+y+z)' = x' * y' * z'
4. (xyz)' = x' + y' + z'
(x*y)' = x' + y'
 ශිල්ප 64
ශිල්ප 64