The rules of Boolean Algebra are:.

every law has two expressions, (a) and (b). This is known as duality. These are obtained by changing every AND (.) to OR (+), every OR (+) to AND (.) and all 1's to 0's and vice-versa.

It has become conventional to drop the . (AND symbol) i.e. A.B is written as AB.

AND Operations (·)
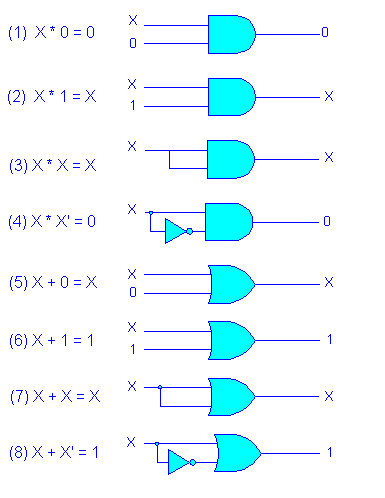
0·0 = 0      A·0 = 0
1·0 = 0      A·1 = A
0·1 = 0      A·A = A
1·1 = 1      A·A' = 0

OR Operations (+)
0+0 = 0      A+0 = A
1+0 = 1      A+1 = 1
0+1 = 1      A+A = A
1+1 = 1      A+A' = 1

NOT Operations (')
0' = 1 A'' = A
1' = 0

Associative Law
(A·B)·C = A·(B·C) = A·B·C
(A+B)+C = A+(B+C) = A+B+C

Distributive Law
A·(B+C) = (A·B) + (A·C)
A+(B·C) = (A+B) · (A+C)

Commutative Law
A·B = B·A
A+B = B+A

Precedence
AB = A·B
A·B+C = (A·B) + C
A+B·C = A + (B·C)

DeMorgan's Theorem
(A·B)' = A' + B' (NAND)
(A+B)' = A' · B' (NOR)

ශිල්ප 64