දැන් අප ප්රස්තාරයක් යනු කුමක්දැයි ඉගන ගනිමු.
ප්රස්තාරයක් යනු යම්කිසි මාන දෙකක හෝ තුනක එම එක් එක් මාන වල අගයන් ලෙස සටහන්වූ ඛන්ඩාංක තලයක ලකුනු කර එම ලක්ෂ්යයන් යා කිරීමෙන් ලැබෙන ශ්රිතය නැතහොත් එම ලක්ෂ්යය යා කිරීමෙන් ලැබෙන වක්රය ප්රස්තාරයකි.
ප්රස්තාරයක අනුක්රමණය කූමක්දැයි විමසා බලමු.
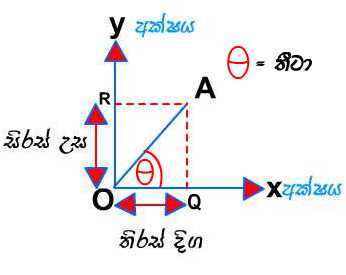
මෙහි ප්රස්තාරයේ ( රේඛාවේ ) අනුක්රමණය වන්නේ = සිරස් උස / තිරස් දිග වේ.
තවද මෙය tanθ = OR / OQ ලෙස ගෙන විසදිය හැක.
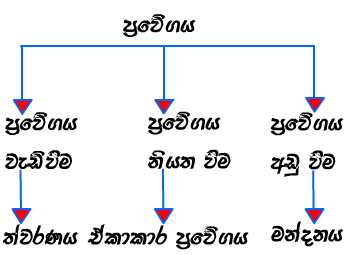
දැන් අප මෙම ප්රවේග ආකාර තුන ප්රවේග-කාල ප්රස්තාරයක ලකුණු කරන ආකාරය ඉගන ගනිමු.
1). අප ප්රථමයෙන් විස්ථාපන කාල ප්රස්තාරයක් මඟින් ප්රවේගය සොයන ආකාරය සොයා බලමු.
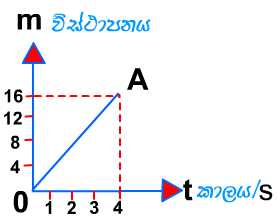
ප්රවේගය = 20m / 4s
එබැවින් ප්රවේගය = 5 ms-1 වේ.
2). දැන් අප ප්රවේග-කාල ප්රස්තාරයක් පිළිබඳව ඉගන ගනිමු.
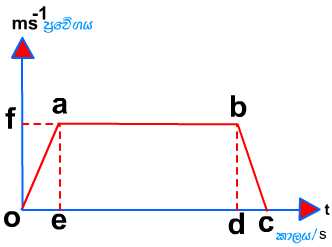
දැන් අප ප්රවේග-කාල ප්රස්තාරය ඇසුරින් ගත හැකි අගයන් පිළිබඳව ඉගන ගනිමු.
1. ත්වරණය = oa රේඛාවේ අනුක්රමණය = of / oe මඟින්ද,
2. ත්වරණයෙන් ගමන් කළ කාලය = oe කාලය මඟින්ද,
3. ත්වරණයෙන් ගමන් කළ දුර = oae ත්රිකෝණයේ වර්එලය මඟින්ද,
4. උපරිම වේගය = f. මඟින්ද
5. ඒකාකාර ප්රවේගයෙන් ගමන් කළ කාලය = ed මඟින්ද,
6. ඒකාකාර ප්රවේගයෙන් ගමන් කළ දුර = abde සෘජුකෝණස්රයේ වර්ග එලය මඟින්ද,
7. මන්දනය = bc රේඛාවේ අනුක්රමණය මඟින්ද,
8. මන්දනයෙන් ගමන් කළ දුර = bcd ත්රිකෝණයේ වර්එලය මඟින්ද,
9. මන්දනයෙන් ගමන් කළ කාලය = cd කාලය. මඟින්ද,
10. ගමන් කළ මුළු දුර = oabc ත්රැපීසියමේ වර්ගඑලය මඟින්ද
ගණනය කළ හැක.
දැන් ඔබට ප්රවේගය සම්බන්දයෙන් දී ඇති ගැටළු වලදී එය ඉතා පහසුවෙන් ප්රවේග-කාල ප්රස්ථාරයක් ආධාරයෙන් විසදිය හැකි බව පෙනෙනු ඇත.
 ශිල්ප 64
ශිල්ප 64