නිමානයේදී ඇස්තමේන්තු අගය හා සත්ය අගය අතර අගයක් ලබාගනී. එහිදී තාර්කික ලෙස අගයන් භාවිතා කරයි.
නියම අගය ලබාගත නොහැකි වූ විට 20 හෝ 21 ලෙස වැනි අගයන් පරාසයක් දෙයි. එය 21 පමණ කියනවාට වඩා තිරය.
මුදල් උදාහරණ :
මහාචාර්ය සමරජීවට බස් ගාස්තු වශයෙන් දිනකට රු. 20 ක්ද, තේ පානය සඳහා රු. 15 ක්ද, දහවල් ආහාරය සඳහා රු. 50 ක්ද, සවස තේ සඳහා රු 20 ක්ද වියදම් වේ. ඔහු ගෙදරින් ගෙන යා යුතු මුදල නිමානය කරන්න.
මුදල=20+15+50+20 = රු 70
දින 5 සතියකට අවශ්ය මුදල = රු. 350
දින 22 මාසයකට = රු. 350 * 22 =7700
කාලය , වේගය හා දුර:
පාපැදි තරඟ කණ්ඩායමක් පැයට කි.මී. 60 ක වේගයෙන් යයි නම් මිනිත්තුවකදී යන දුර ?
පැයකට මිනිත්තු 60 බැවින් දුර=කි.මී. 60/60 = 1 කි.මී.
මාතලේ නගරයෙන් තරඟ කණ්ඩායම පිටත් වූයේ පෙ.ව 7.50 ටය. ඔවුන් කි.මී. 45 ක් දුරින් පිහිටි නාවුල නගරයට ලඟාවන්නේ කීයටද ?
මිනිත්තුවට යන දුර 1 කි.මී නිසා
කි.මී 45 කට කාලය = මිනිත්තු 45
නාවුලට පැමිනෙන වේලාව = 7:50 + 00:45= 8:35
බර
ලොරියකට බර පිළිවෙලින් 60kg, 65kg, 70kg වූ සීනි මිටි 50 ක් කවලමේ පටවන ලදි. පැටවූ සීනි ප්රමාණය කොපමණද ?
මෙහිදී සියලුම මිටි ගණන 50 කි.
මිටි 50 විවිධ ආකාරයෙන් 60kg, 65kg, 70kg මිටි අතර බෙදිය හැකිය.
(10:20:20 හෝ 15:10:25 හෝ 50:0:0 හෝ 0:50:0 වැනි)
එමනිසා නියමම අගයක් ප්රකාශ කළ නොහැක.
එහිදී අගය නිමානය කළ යුතුය.
බර සාමාන්ය අගය =(60kg+65kg+70kg)/3=65g
මිටි 50 බැවින් මුලු බර=65kg*50=3250kg
අවම බර = 60kg * 50 = 3000kg
උපරිම බර= 70kg * 50 = 3500kg
සාමාන්ය බර == 3500kg
පිළිතුර 3000kg හා 3500kg අතර අගයක් විය හැක.
ද්රව පරිමාම
බෙහෙත් වෙලෙන්ඳකු ලඟ ලීටර 1.5 ක තෙල් බෝතල් දෙකක තිබූ තෙල් 80ml කුඩා බෝතල් වලට පුරවන ලදි.
පිරවිය හැකි තෙල් කුප්පි ප්රමාණය කීයද? ඉතිරි වන තෙල් ප්රමාණය කොපමණද ?
බෝතල් දෙකේම තෙල් ප්රමාණය = (1.5 * 2)* 1000ml
(අගයන් සියල්ල එකම ඒකකයට හරවා ගැනීම ඉතා වැදගත්ය)
කුප්පි ගණන = (3000/80)ml=37.5 කුප්පි
(නිතරම ඒකකය ලියන්න)
කුප්පි ගණන=37
ඉතිරිවන ප්රමාණය (80*0.5)=40ml
මධ්යන්ය (mean)
නිමාලි විෂයන් 6 කට 88,72, 65, 53, 49, 37 බැගින් ලකුණු ගත්තාය . ලකුණුවල මධ්යන්ය සොයන්න.
මධ්යන්ය=(88+72+65+53+49+37)/6
=60.66
මුදල් උදාහරණ :
මහාචාර්ය සමරජීවට බස් ගාස්තු වශයෙන් දිනකට රු. 20 ක්ද, තේ පානය සඳහා රු. 15 ක්ද, දහවල් ආහාරය සඳහා රු. 50 ක්ද, සවස තේ සඳහා රු 20 ක්ද වියදම් වේ. ඔහු ගෙදරින් ගෙන යා යුතු මුදල නිමානය කරන්න.
මුදල=20+15+50+20 = රු 70
දින 5 සතියකට අවශ්ය මුදල = රු. 350
දින 22 මාසයකට = රු. 350 * 22 =7700
කාලය , වේගය හා දුර:
පාපැදි තරඟ කණ්ඩායමක් පැයට කි.මී. 60 ක වේගයෙන් යයි නම් මිනිත්තුවකදී යන දුර ?
පැයකට මිනිත්තු 60 බැවින් දුර=කි.මී. 60/60 = 1 කි.මී.
මාතලේ නගරයෙන් තරඟ කණ්ඩායම පිටත් වූයේ පෙ.ව 7.50 ටය. ඔවුන් කි.මී. 45 ක් දුරින් පිහිටි නාවුල නගරයට ලඟාවන්නේ කීයටද ?
මිනිත්තුවට යන දුර 1 කි.මී නිසා
කි.මී 45 කට කාලය = මිනිත්තු 45
නාවුලට පැමිනෙන වේලාව = 7:50 + 00:45= 8:35
බර
ලොරියකට බර පිළිවෙලින් 60kg, 65kg, 70kg වූ සීනි මිටි 50 ක් කවලමේ පටවන ලදි. පැටවූ සීනි ප්රමාණය කොපමණද ?
මෙහිදී සියලුම මිටි ගණන 50 කි.
මිටි 50 විවිධ ආකාරයෙන් 60kg, 65kg, 70kg මිටි අතර බෙදිය හැකිය.
(10:20:20 හෝ 15:10:25 හෝ 50:0:0 හෝ 0:50:0 වැනි)
එමනිසා නියමම අගයක් ප්රකාශ කළ නොහැක.
එහිදී අගය නිමානය කළ යුතුය.
බර සාමාන්ය අගය =(60kg+65kg+70kg)/3=65g
මිටි 50 බැවින් මුලු බර=65kg*50=3250kg
අවම බර = 60kg * 50 = 3000kg
උපරිම බර= 70kg * 50 = 3500kg
සාමාන්ය බර == 3500kg
පිළිතුර 3000kg හා 3500kg අතර අගයක් විය හැක.
ද්රව පරිමාම
බෙහෙත් වෙලෙන්ඳකු ලඟ ලීටර 1.5 ක තෙල් බෝතල් දෙකක තිබූ තෙල් 80ml කුඩා බෝතල් වලට පුරවන ලදි.
පිරවිය හැකි තෙල් කුප්පි ප්රමාණය කීයද? ඉතිරි වන තෙල් ප්රමාණය කොපමණද ?
බෝතල් දෙකේම තෙල් ප්රමාණය = (1.5 * 2)* 1000ml
(අගයන් සියල්ල එකම ඒකකයට හරවා ගැනීම ඉතා වැදගත්ය)
කුප්පි ගණන = (3000/80)ml=37.5 කුප්පි
(නිතරම ඒකකය ලියන්න)
කුප්පි ගණන=37
ඉතිරිවන ප්රමාණය (80*0.5)=40ml
මධ්යන්ය (mean)
නිමාලි විෂයන් 6 කට 88,72, 65, 53, 49, 37 බැගින් ලකුණු ගත්තාය . ලකුණුවල මධ්යන්ය සොයන්න.
මධ්යන්ය=(88+72+65+53+49+37)/6
=60.66
පහත දැක්වෙන බිත්තියේ පාට කල කොටසට ඇල්ලීමට එකක් 20 20 වූ පිඟන් ගඩොල් කීයක් අවශ්යද. පිඟන් ගඩොල් කොටස් අපතේ නොයන බව සලකන්න.
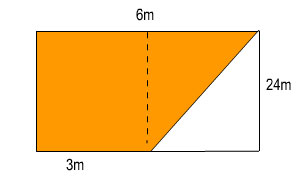
හිස් කොටස බිත්තියේ 1/2 ක කොටසින් අඩක් බව පෙනේද?
එමනිසා අවශ්ය වර්ගඵලය බිත්තියෙන්
(1/2) + (1/2)/2= 3/4
එමනිසා අවශ්ය වර්ගඵලය බිත්තියෙන්
(1/2) + (1/2)/2= 3/4
බිත්තියේ මුලු වර්ගඵලය=(6*100cm)* (3*100cm)=600*300
පිඟන් ගඩොල් සඳහා වර්ගඵලය=(600*300)cm² *(3/4)
=150*300*3
=150*300*3
පිඟන් ගඩොලක වර්ගඵලය=20cm *20cm=400cm²
පිඟන් ගඩොල් ගණන=(150*300*3)cm²/400cm²
පිඟන් ගඩොල් ගණන=(150*300*3)cm²/400cm²
=(150*3*)/4=450/4=112.5
≈113
≈113
ආසන්න අගයට නිමානය
දශම අගයන් සැකීමේදී දශමස්ථාන කොටසේ 0.5ට අඩු සංඛ්යා වලින් දශම ගණන ඉවත් කිරීමත්,
0.5 හෝ ඊට වැඩිනම් ආසන්න ධන පූර්ණ සංඛ්යාවටත් ගැනීම කරයි.
දශම අගයන් සැකීමේදී දශමස්ථාන කොටසේ 0.5ට අඩු සංඛ්යා වලින් දශම ගණන ඉවත් කිරීමත්,
0.5 හෝ ඊට වැඩිනම් ආසන්න ධන පූර්ණ සංඛ්යාවටත් ගැනීම කරයි.
111.45 = 111
111.38 = 111
111.97 = 112
111.85 = 111
111.50 = 112
111.38 = 111
111.97 = 112
111.85 = 111
111.50 = 112
මේ අනුව සංඛ්යාවක අගය විශාල වීමත් සමගම අත හරින හෝ එකතු කරන අගයන් එතරම් බල නොපායි.
11,386,906 ආසන්න 10ට, 100ට, 1000ට, 10000ට , 100,000ට හා මිලියනයට වටයන්න.
11,386,906 ආසන්න 10 ට = 11,386,910
11,386,906 ආසන්න 100 ට = 11,386,900
11,386,906 ආසන්න 1,000 ට = 11,387,000
11,386,906 ආසන්න 10,000 ට = 11,390,000
11,386,906 ආසන්න 100,000 ට = 11,400,000
11,386,906 ආසන්න 1,000,000 ට = 11,000,000 මෙහිදී මිලියන 11.4 යන්නද ගත හැක.
11,386,906 ආසන්න 100 ට = 11,386,900
11,386,906 ආසන්න 1,000 ට = 11,387,000
11,386,906 ආසන්න 10,000 ට = 11,390,000
11,386,906 ආසන්න 100,000 ට = 11,400,000
11,386,906 ආසන්න 1,000,000 ට = 11,000,000 මෙහිදී මිලියන 11.4 යන්නද ගත හැක.
 ශිල්ප 64
ශිල්ප 64