ඝනක වල විවිධ ජ්‍යාමිතික හැඩ සහිත පතුලක් (base) තිබිය හැක.
එහිදී එම ඝනය සිලින්ඩරාකාර නම් එහි පතුලේ වර්ගඵලය උසින් ගුණ කිරීමෙන් එහි පරිමාව ලබාගත හැක.
V=Bh
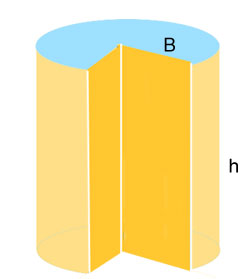
පතුලෙන් සෘජු කෝණයක් සිටින සේ කොටස් කපා ඉවත් කල සිලින්ඩරය අධ්‍යයනය කරන්න. එහි පරිමාව සෙවීමට පතුලේ වර්ගඵලය සෙවීම කල යුතුයි.
එ‍ලෙසින්ම එහි 90° කොටසක් ඉවත් කර ඇති නිසා වර්ගඵලය 1/3 එක බවද කිය හැකිය.
ඒ අනුව පරිමාව සම්පූර්ණ සිලින්ඩරයේ පරිමාවෙන් 3/4 බවද කිය හැකිය.
මේ ආකාරයටම සංකීර්ණ වස්තුවල පරිමා ගණනය කල හැක. ඔබ කලයුත්තේ තර්කානුකූලව සිතීමයි.
එවිට ප්‍රශ්නය සරළ වේ.
එවිට ප්‍රශ්නය සරළ වේ.
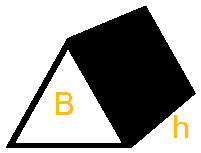
මතු පිට වර්ගඵල සැලකීමේදී ඝනය මතුපිට සෑදී ඇති සරළම ජ්‍යාමිතික රූප වලට වෙන් කර ගත යුතුය.
එනම් සෘජු කෝණී ත්‍රිකෝණ , වෘත්ත හා සෘජු කෝණාස්‍ර වලටය.
ත්‍රිකෝණයක වර්ගඵලය = (උස x පළල)1/2
සෘජු කෝණාස්‍රයක වර්ගඵලය = (උස x පළල)
වෘත්යක වර්ගඵලය = π(r)²
සෘජු කෝණාස්‍රයක වර්ගඵලය = (උස x පළල)
වෘත්යක වර්ගඵලය = π(r)²
ශිල්ප 64