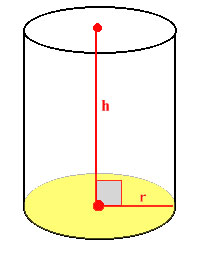
සිලින්ඩරයක පරිමාව මැනීමේදී එහි උස සහ පතුලේ වර්ගඵලය වැදගත් වේ. පතුලේ වර්ගඵලය සොයාගැනීමට වෘත්තයක වර්ගඵලය පිළිබඳ සමීකරණය භාවිතා කරයි.

පතුලේ වර්ගඵලය=(π) x (r²)=πr² ( r= වෘත්තයේ අරය)
සිලින්ඩරයේ පරිමාව=h x (πr²)=hπr²

සිලින්ඩරයේ මතුපිට වර්ගඵලය සේවීමද පහසුය.
සිලින්ඩරයේ වෘත්තයේ පරිමිතිය සලකා බලා (π x 2 x r)=2πr
වෘත්තයේ පරිමිතිය x (h) =2πr
සිලින්ඩරයේ පිටත වර්ගඵලය=2πrh
වෘත්තමය පතුලේ හා ඉහළ වර්ගඵලය = πr²
සිලින්ඩරයේ මතුපිට වර්ගඵලය=2πrh+2(πr²) වේ.

මෙහිදී අප වෘත්තය හා සෘජුකෝණාස්‍රය පිළිබඳ අප දන්නා දැනුම එම ජ්‍යාමිතික ලක්‍ෂණ සහිත සිලින්ඩරයකට ආදේශ කළෙමු.

මෙම සිලින්ඩරයේ ලකුණු කල නව රේඛා දිගේ කැපීමෙන් ලබාගත හැකි ඝන වල පරිමාවන් සෙවීමට ඔබට පුලුවනිද ?

ඒ සඳහා සිලින්ඩරයේ පරිමාව ගණනය කර පසුව අදාල කොටසේ අනුපාතය හෝ භාගය ගණනය කරමු.

මෙම සිලින්ඩරයේ උස h නම් හා
පතුලේ අරය r නම්ද
v=hπr² සමීකරණය භාවියෙන්

hπr²/2

hπr²/4

hπr² (3/4)

යන සමීකරණ ලබාගත හැකිය.

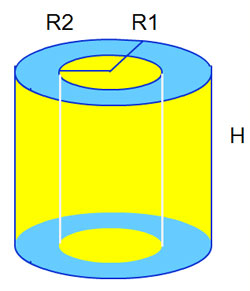දැන් මේ සිලින්ඩරය අධ්‍යයනය කරන්න. එහි මැදින් නම් අරයක් ඇති සිලින්ඩරයක් ඉවත් කර ඇත.

ඉතිරිවන සිලින්ඩරයේ පරිමාව v3=v1-v2
v3=hπR1² - hπR2²

v3=hπ(R1² -R2²)

 

 

 

 

පහත දක්වන සිලින්ඩරයේ කොටසක් ඉවත් කරනු වෙනුවට තවත් සිලින්ඩරයක එකතු කර ඇත. එහි පරිමාව සොයමු.
මෙහිදී තෙවන සිලින්ඩරයේ දිග h2 ලෙස සලකමු.

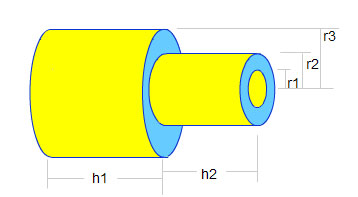
විශාල සිලින්ඩරයේ පරිමාව v1=h1π(r3)²

කුඩා සිලින්ඩරයේ පරිමාව v2=h2π(r2)²

කුඩාම සිලින්ඩරයේ පරිමාව v3=h2π(r1)²

සම්පූර්ණ පරිමාව=v1+(v2-v3)
සම්පූර්ණ පරිමාව=h1π(r3)²+h2π(r2)² - h2π(r1)²

මෙහිදි නියත අගයන් ආදේශනය කර අපට අගය ලබාගැනීමට පුලුවන.