පහත දැක්වෙන්නේ π අගය නිර්මාණය වීම සඳහා ඔහු ඉදිරිපත් කළ කරුණුය.


වෘත්තයක වර්ගඵලය සෙවීමේදී ඔහුට 1% ක නිරවද්‍යතාවයක් ලබාගත හැකි විය.
 වෘත්තයක අන්තර්ගත ශඩාස්‍රයක වර්ගඵලය වෘත්තයේ වර්ගඵලයට වඩා අඩුබව ඔහු නිරීක්‍ෂණය කළේය.

ශඩාස්‍රයක වර්ගඵලය එහි අන්තර්ගත පාදය ඒකක 1 ක් වූ සමපාද ත්‍රිකෝණ 6 ක වර්ගඵලයට සමාන වන බව ඔහු නිරීක්‍ෂණය කළේය.

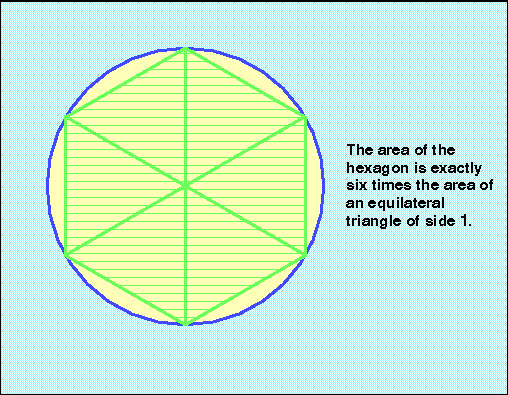
 ඒ අනුව එම ත්‍රිකෝණයේ වර්ගඵලය 
 =(1/2) x 1 x (√3/2)=2.598කි
 
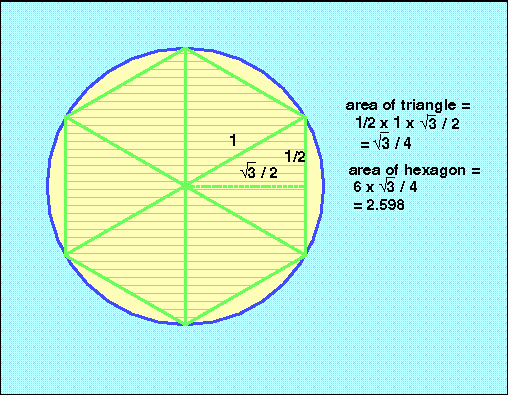
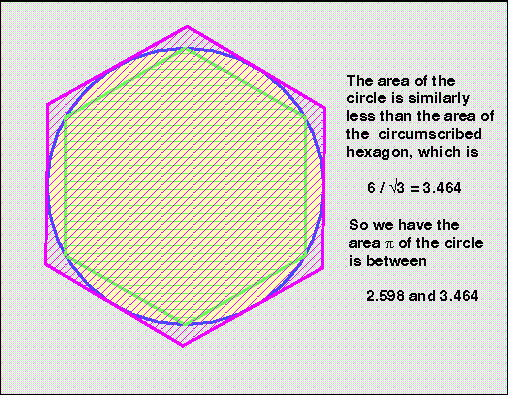
වෘත්තයට පිටින් ඇඳි ශඩාස්‍රයේ වර්ගඵලය 3.464 බැවින්.
වෘත්තයේ වර්ගඵලය 2.598 හා 3.464 අතර වන බව ඔහු පැවසුවේය.

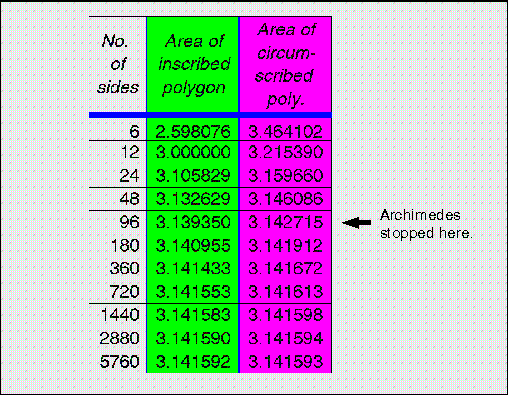
 මේ අනුව පාද ගණන වැඩි කරමින් වෘත්තයේ වර්ගඵලය සෙවීමට උත්සාහ දැරූ ආකිමිඩීස්
 ලබාගත් දත්ත අනුව අරය 1 ක් වූ වෘත්තයක වර්ගඵලය 3.142715 ලෙස ඉදිරිපත් කලේය.