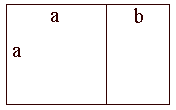
අර්ථ දැක්විමෙන් රන්මය අනුපාතය වන්නේ
a/b = (a+b)/a
a/b=1/2+√(5)/2
1.61803398875 . . .


ඊජිප්තු පිරමිඩවල  ඇල උස හා පාදයේ දිග අතර s:b අනුපාතය රන්මය අනුපාපතය ලෙස හඳුන්වයි (golden ratio).

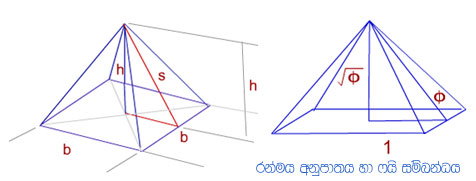
උස = 146.515 m හා පාදය = 230.363 m වූ චියෝප්හි පිරමිඩය සැලකීමෙන්
පාදයේ දිගින් අඩ = 230.363 ÷ 2 = 115.182 m

එම නිසා පයිතරස් ප්‍රමේයෙන්
s²=(146.515)² + (115.182)² = 34,733 m²
s = 186.369 m

ඇල උස s පාදයේ අඩකින් බෙදීමෙන්
Φ=186.369 ÷ 115.182 = 1.61804


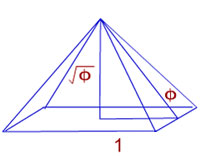
මේ අනුව ඊජිප්තු ත්‍රිකෝණයේ 1 :√Φ : Φ අනුපාතයක් තිබේ.

පයිතගරස් ප්‍රමේය භාවිතයෙන් h² = Φ² - 1²
h = Φ² - 1²

පසුව තාරකා විද්‍යාඥයක වූ කෙප්ලර් මේ අනුපාතය අගය කරමින් තම සොයාගැනීම් විස්තර කිරීමට භාවිතා කළේය.
මේ අතරම පිරමිඩ වල පාදයන් සමාන බවත් ඒවායේ පරිමිතිය යම් වෘත්තයක පරිමිතියට සමාන වන බවද,
එහි පාදයේ වර්ගඵලය දෙනලද වෘත්තයක වර්ගඵලයකට සමාන බවද සොයා ගැනිණි.

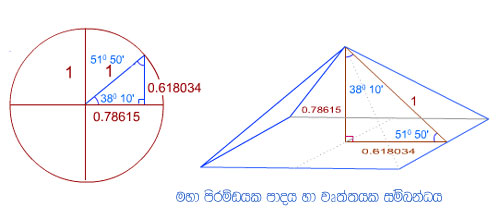
පරමිඩයේ උස =√Φ නම්
පතුලේ පරිමිතිය = 4 x 2 = ඒකක 8
වෘත්තයේ පරිමිතිය = 2π √Φ= 7.992
මේ අනුව 0.1% තරම් ආසන්න බවක් පිරමිඩයේ පතුලේ පරිමිතිය හා වෘත්තයක පරිමිතිය අතර තිබෙන බව පෙන්විය හැක.

ඒ අනුව වෘතතයක පරිමිතිය සලකා
2π √Φ= 8
π=(4/1.272)=3.146 බව පෙන්විය හැක.

පතුලේ වර්ගඵලය = 2*(√Φ)*(2)=5.088
අරය √Φ වූ වෘත්තයක ක්‍ෂේත්‍රඵලය = πr² භාවිතයෙන්
π(√Φ)² =5.083
මෙය ඉතා ආසන්න අගයකි.

මේ අනු අතීත ඊජිප්තුයානුවන් π අනුපාතය භාවිතා කළ බවට සිතිය හැක.