සංඛ්‍යා රටාවල අපට හමුවන ඉතාම ආශ්වාදජනක විසඳුමක් නම් පැස්කල් ත්‍රිකෝණයයි. එය පරිගණක තාක්‍ෂණයේ මුලිකයෙකු ලෙස හැඳින්වෙන බ්ලේසි පැස්කල් නම් ප්‍රංශ ගණිතඥයා සිහිපත් කරයි.
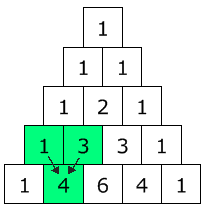
ත්‍රිකෝණය සෑදීමට 1 න් පටන්ගන්න, පසුව ත්‍රිකෝණාකාරව විහිදාලන්නේ සැම අංකයකම අගය, ඊට ඉහලින් ඇති සංඛ්‍යා දෙකේ එකතුවයි.
ලකුණු කර ඇති පරිදි 1+3 = 4 වේ.
දිගටම මෙය පිටවීමෙන් ඉතාමත් වැදගත් සංඛ්‍යා රටා ලබාගත හැක.
පැස්කල් ත්‍රිකෝණයේ විවිධ සංඛ්‍යා රටා
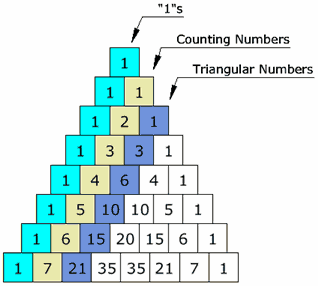
විකර්ණ Diagonalsප්‍රථම විකර්ණය "1" ඒවාය ,
දෙවැනි විකර්ණය 1,2,3,... වේ
තෙවැනි විකර්ණය ත්‍රිකෝණ සංඛ්‍යා වේ
පෙන්වා නොමැති හතරවන විකර්ණයේ
එන්නේ tetrahedral සංඛ්‍යා වේ
ඔත්තේ සහ ඉරට්ටේ සංඛ්‍යා
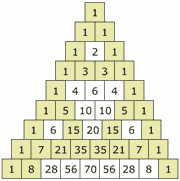
තිරස් පේළියේ එකතුව
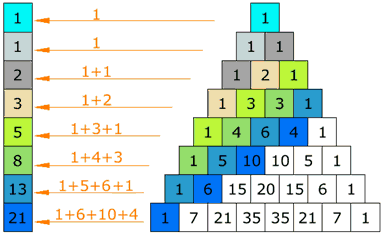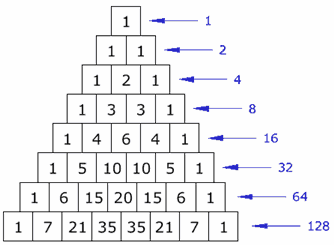
ෆයිබොනාසි රටාව Fibonacci Sequenceෆයිබොනාසි රටාව සැකසෙන්නේ රූපයේ පරිදි පෙර සංඛ්‍යා දෙකක් එකතු කිරීමෙනි.
උදා : 3+5=8, අනතුරුව 5+8=13, ... ආදී වශයෙනි
ශිල්ප 64