ඕනෑම ඡ්‍යාමිතික ඝන වස්තුවක් ගත්විට එය පෘෂ්ඨ වලින් සමන්විත වේ. එම එක් එක් පෘෂ්ඨය ඡ්‍යාමිතික තල රූපයකි. පෘතුවිය ආසන්නව ගෝලයකි. එහි පෘෂ්ඨය මත අප වාසය කරමු. එහි මුහුදු, විල්, ගංගා කැලෑ සහ නගර වෙන වෙනම ජ්‍යාමිතික රූප සාදන බව ඔබ දනී.
කිසියම් ඡ්‍යාමිතික ඝන වස්තුවක එක් එක් පෘෂ්ඨයේ වර්ගඵලය සොයා ඒ සියල්ල එකට එකතුකිරීමෙන් වස්තුවේ මුළු පෘෂ්ඨ වර්ගඵලය ගණනය කලහැකි බවද ඔබ දනී.
උදාහරණ:
ඝනකයක් ගත්විට එහි පෘෂ්ඨය සමචතුරශ්‍රයකි.එම සමචතුරශ්‍රයේ මුළු පෘෂ්ඨ වර්ගඵලය ගණනය කර ,ඝනකයේ සමචතුරශ්‍ර ගණනින් එනම් 6න් ගුණකලවිට ඝනකයේ මුළු පෘෂ්ඨ වර්ගඵලය ලැබේ.
ඝනකයක් ගත්විට එහි පෘෂ්ඨය සමචතුරශ්‍රයකි.එම සමචතුරශ්‍රයේ මුළු පෘෂ්ඨ වර්ගඵලය ගණනය කර ,ඝනකයේ සමචතුරශ්‍ර ගණනින් එනම් 6න් ගුණකලවිට ඝනකයේ මුළු පෘෂ්ඨ වර්ගඵලය ලැබේ.
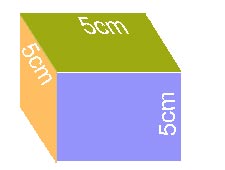
මෙම ඝනකයේ පැත්තක දිග 5cm වේ.
එමනිසා එහි එක් පෘෂ්ඨයක වර්ගඵලය = 5cm × 5cm
= 25 cm²
ඝනකයේ මුළු පෘෂ්ඨ වර්ගඵලය =225 cm² × 6
= 1350 cm²
පහත 5, 10, 20 උස, දිග හා පළල ඇති ඝණකාභයේ මතුපිට වර්ගඵලය සොයන අයුරු බලන්න. සාමාන්‍ය ජීවිතයේදී එය තෑගි පෙට්ටියක මතුපිට අලවන්නට ගන්නා කඩදාසි ප්‍රමාණය වැනි උදාහරණයක්ද විය හැක.
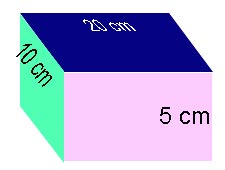මෙහිදී එක හා සමාන පෘෂ්ඨ දෙකක් බැගින් පෘෂ්ඨ යුගල තුණක් තිබෙන බව ඔබට පෙනෙනවාද? ඔබට නොපෙනෙන පෘෂ්ඨ තුන පෙනෙන පෘෂ්ඨ වලට සමාන බව ඔබට හැඟේද?
මෙහිදී එක හා සමාන පෘෂ්ඨ දෙකක් බැගින් පෘෂ්ඨ යුගල තුණක් තිබෙන බව ඔබට පෙනෙනවාද? ඔබට නොපෙනෙන පෘෂ්ඨ තුන පෙනෙන පෘෂ්ඨ වලට සමාන බව ඔබට හැඟේද? මේ අනුව පෙනෙන එක් එක් පෘෂ්ඨ වල වර්ගඵලය වන්නේ සෙ.මී.
10 * 20 =200
10 * 5=15
5 * 20 =25
10 * 20 =200
10 * 5=15
5 * 20 =25
නොපෙන පැති මෙම එකතු එනම් 240 ට සමාන වේ.
මේ බව ගෙදරදි හමුවන කුඩා පෙට්ටිවලින් ගණණය කර බලන්න.
එකම බරැති දූරියන් ගෙඩියක හෝ වට්ටක්කා ගෙඩියක මතුපිට වර්ගඵලය වැඩි කුමකද?
ශිල්ප 64