කිසියම් සංඛ්යාවක් ගත්විට එම සංඛ්යාව ආශ්රයෙන් ත්රිකෝණයක් පිළියෙල කල හැකිනම් එය ත්රිකෝණ සංඛ්යාවක් නම් වේ.
උදාහරණ. 1 3 6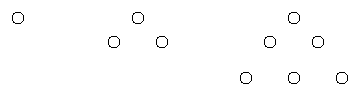
අභ්යාස.
(1) පලමු ත්රිකෝණ සංඛ්යා 6 ලියන්න.
(2) n වන ත්රිකෝණ සංඛ්යාව සෙවීමට සූත්රයක් ගොඩනගන්න.
(3) 10 වන ත්රිකෝණ සංඛ්යාව සොයන්න.
(4) 50 වන ත්රිකෝණ සංඛ්යාව සොයන්න.
(3) 10 වන ත්රිකෝණ සංඛ්යාව සොයන්න.
(4) 50 වන ත්රිකෝණ සංඛ්යාව සොයන්න.
මේ සඳහා 1 , 3 , 6 රටාව අධ්යනය කර බලන්න.
1 ට 2 ක් එකතු වී 3 සෑදේ.
3 ට තව 3 ක් එකතු වී 6 සෑදේ.
ඊ ලඟ මට්ටමේදී ත්රිකෝණය සම්පූර්ණ වීමට බිංදු 5 ක් අවශ්යය.
එනම් 6 ට 5 ක් එකතුවිය යුතුය. එය 11 කි
1 ට 2 ක් එකතු වී 3 සෑදේ.
3 ට තව 3 ක් එකතු වී 6 සෑදේ.
ඊ ලඟ මට්ටමේදී ත්රිකෝණය සම්පූර්ණ වීමට බිංදු 5 ක් අවශ්යය.
එනම් 6 ට 5 ක් එකතුවිය යුතුය. එය 11 කි
මෙහිදී වැඩිවන ගණන රටාවක් ලෙස ගත්විට 2, 3 , 5 වේ.
ඊ ලඟ ත්රිකෝණ සඳහා එය 7, 9 ලෙස එකතුවන බව ඔබට පෙනේද.
ඊ ලඟ ත්රිකෝණ සඳහා එය 7, 9 ලෙස එකතුවන බව ඔබට පෙනේද.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||||||
| 1 | 3 | 6 | 11 | 18 | 27 | 38 | 51 | 66 | 83 | |||||||||
| 2 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
 ශිල්ප 64
ශිල්ප 64