මීටර් 2, 3, හා 4 ප්රමාණයේ වූ ලී පෙට්ටියක දිගම රේඛාව කොපමණ දිගද ? මේ අනුව ඝණකයක පාද තුනේ දිගවල වර්ගයන්වල එකතුව
පයිතගරස් ප්රමේයය යෙදුම් වැඩි දුරටත්
පහත සංඛ්යා රටාව බලන්න
3 4 5
5 12 13
7 24 25
9 40 41
11 60 61
13 84 85
15 112 113
17 144 145
19 180 181
21 220 221
23 264 265
25 312 313
4 3 5
6 8 10
8 15 17
10 24 26
12 35 37
14 48 50
16 63 65
18 80 82
20 99 101
22 120 122
24 143 145
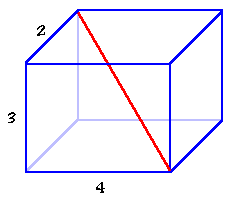
මෙය විසඳීම සඳහා සෘජුකෝණික ත්රිකෝණ දෙකක් ඇඳගන්න
BCD ත්රිකෝණයේ
BD²=BC² + CD² : CD දන්නා නිසා BC සොයාගත යුතුය
ABC ත්රිකෝණයේ
BC² = AB² + AC²
BC² = (4)² + (2)²
BD²=BC² + CD²
BD²=(4)² + (2)² +(3)²
BD=5.38
එහි දිගම රේඛාවේ වර්ගය වන බව පෙනේ.
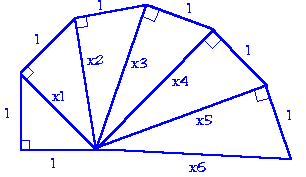
x1=(1)² + (1)² = √2
x2= (1)² + (√2)² = √3
x3= (1)² + (√3) ² = √4
x4= (1)² + (√4) ² = √5
x5= (1)² + (√5) ² = √6
x6= (1)² + (√6) ² = √7
x7= (1)² + (√7) ² = √8
මෙය සංඛ්යා රටාවකි
 ශිල්ප 64
ශිල්ප 64