සෘජුකෝණී ත්‍රිකෝණයක් ඇඳ, එහි පාදවල දිගට සමචතුරශ්‍ර තුනක් අඳින්න. මධ්‍යම ප්‍රමාණයේ සමචතුරශ්‍රය මත දක්වා ඇති පරිදි ඉරි ඇඳ කපාගන්න.
ඒවා රෑපයේ පෙන්වා ඇති පරිදි තබා බලන්න.
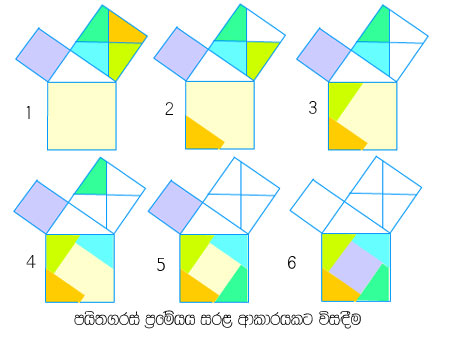
තවත් ක්‍රමයක් සලකා බලමු
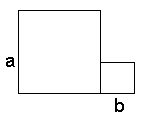
a හා b ප්‍රමාණ දෙකකින් යුතු සමචතුරස්‍ර දෙකක් කපා එකලඟ තබන්න. කුඩාම පාදය b වනසේ සෘජු කෝණික ත්‍රිකෝණ දෙකක් ඇඳ කපාගන්න. .
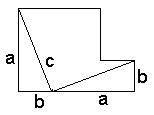
ඒවා වමට සහ දකුණට කරකවා සෑදෙන සම චතුරස්‍රයේ වර්ගපලය බලන්න
තවත් ක්‍රමයක් සලකා බලමු
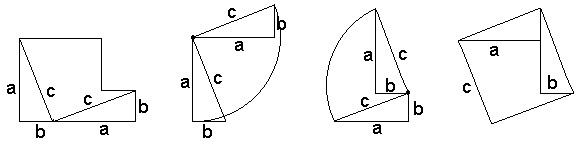
එකහා සමාන සෘජුකෝණී ත්‍රිකෝණ 4ක් කපාගෙන පහත පරිදි තබා
භ්‍රමණය කර c දිග පළල ඇති සමචතුරස්‍රයක් සදාගන්න
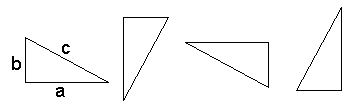
ඒවා වමට සහ දකුණට කරකවා සෑදෙන සම චතුරස්‍රයේ වර්ගපලය බලන්න
තවත් ක්‍රමයක් සලකා බලමු
එකහා සමාන සෘජුකෝණී ත්‍රිකෝණ 4ක් කපාගෙන පහත පරිදි තබා
භ්‍රමණය කර c දිග පළල ඇති සමචතුරස්‍රයක් සදාගන්න
සෑම ත්‍රිකෝණයකම වර්ගපලය (axb)/2 වේ.
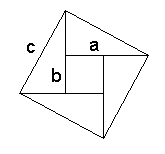විශාල සමචතුරස්‍රය තුල ඇති කුඩා සමචතුරස්‍රාකාර
සිදුරේ දිග හා පළල (a-b) වේ.
එහි වර්ගපලය (a-b) ²
ත්‍රිකෝණ හතරේ වර්ගපලය 4 x (ab/2)
නැතහොත් 2ab වේ.
විශාල සමචතුරස්‍රය තුල ඇති කුඩා සමචතුරස්‍රාකාර සිදුරේ දිග හා පළල (a-b) වේ.
එහි වර්ගපලය (a-b) ²
ත්‍රිකෝණ හතරේ වර්ගපලය 4 x (ab/2)
නැතහොත් 2ab වේ.
සම්පුර්ණ වර්ගපලය c² බැවින්
c² = (a-b)²+2ab වේ
c²= a²+b²-2ab+2ab වේ
c²= a²+b² වේ
ශිල්ප 64