ක්‍රි:පූ 580-500 අතර කාලයේ විසූ ග්‍රීක දාර්ශනිකයෙකු හා ශ්‍රේෂ්ඨ ගණිතඥයකු වූ පයිතගරස් විසින් ඍඡුකෝණී ත්‍රිකෝණයක පාදවල දුර අතර සම්බන්ධයක් පෙන්වා දෙන ලදී.

යස 23 සිට පයිතගරස් ඊජිප්තුවේ පිරමීඩ හා සම්බන්ධ ගණිත ක්‍රම එහි පූජකවරුන් ගෙන් උගත්තේය. තවත් වසර 21 කට පසු ඉතාලියේ ක්‍රෝටන් නගරයට පැමිණි ඔහු විසින් ගණිත පාසලක් ආරම්භ කලේය. ඔහු විසින් හඳුන්වාදෙනු ලැබූ මෙම ගණිත ක්‍රමය අදද ජ්‍යාමිතික ගණනය කිරීම්වල වල පදනම වේ.

එකල්හි මිසර ජාතිකයෝ සමාන දුරින් ගැට 12 ක් ගැසූ ලණුවක් සෘජු කෝණ සහිත ත්‍රිකෝණ මැනීමට යොදාගත්හ.

ඔවුන් එම ලණුව උපකාරයෙන් පිරමිඩ තැනීමේදී සෘජු කෝණාශ්‍ර හා සම්බන්ධ විවිධ ගණනය කිරීම් කළහ.

රේඛා දෙකක් අතර අංශක 90 ක් සහිත වූ විට එය සෘජු කෝණයක් වේ.

 

සෘජු කෝණයක රේඛා දෙක කැපී යන ලෙස රේඛාවක් ඇඳමෙන් සෑදෙන ත්‍රිකෝණය සෘජු කෝණී ත්‍රිකෝණයක් වේ.

එම රේඛාව  (c) කර්ණය ලෙස ජ්‍යාමිතිය හා ත්‍රිකෝණමිතියේදී හඳුන්වයි.


මිසර පිරමීඩවල ඇත්තේ සෘජු කෝණී ත්‍රිකෝණ මත බව අමතක නොකරන්න.

රෑපයේ ඇති පිරමිඩයේ අවම වශයෙන්
සෘජු කෝණී ත්‍රිකෝණ 28ක් වත් දැකිය හැකි බව
ඔබට පෙනෙනවාද ?






පයිතගරස් විසින් ඍඡුකෝණී ත්‍රිකෝණයක පාදවල දුර අතර හඳුන්වා දුන් සම්බන්ධය නම්

ඍඡුකෝණී ත්‍රිකෝණයක a, b, c, නම් පාද මත අඳින සමචතුරස්‍ර A, B, C නම් A හි වර්ගපලය B සහ C වර්ගපල වල එකතුවට සමාණ වේ.

 

වර්ගපලය A = a x a = a²
වර්ගපලය B = b x b = b²
වර්ගපලය C = c x c = c²

 

a² = b² + c²
c  =√(a²+b²)

      

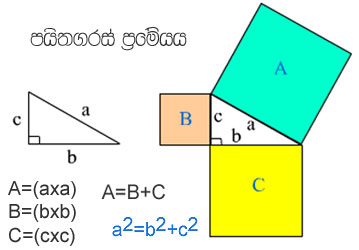
පයිතගරස් ප්‍රමේයට අනුව සෘජු කෝණි ත්‍රිකෝණයක පාද දෙකක් දන්නා විට
අනික් පාදයේ දිග ගණනය කල හැක

a²=c²-b²
b²=c²-a²