ස්වයං පේ්රරතාව සහ සංඛ්යාංකය
13.3 සහ 13.4 චිත්රවලින් දැක්වෙන ප්රස්තාර දෙක එක්තැන් කොට 13.5 (අ) ප්රස්ථාරයෙහි දැක්වේ. මෙම ප්රස්තාරයෙහි t2 සහ t5 ධාරාව උපරිමයට පැමිණ අචලව ගලන කාල වෙයි. t2 සහ t5කාල ගත විටම ඉඩ නොහැර ධාරාව උපරිමයට පැමිණි විගස විස්න්ධි කොට , ශුන්ය වු විගස දිශාව වෙනස් කොට නැවත ඉහත පරිදිම විසන්ධි කළහොත් (ආ) චිත්රයෙහි A ප්රස්ථාරය ලැබෙයි. මෙම ප්රස්තාරය ප්රත්යාවර්ත ත්රිකෝණ තරංගයට සමාන වෙයි. ඉන්පසු A ප්රස්තාරය ජනිත කිරිමට ගත කල කාලය අඩකින් අඩුකරන ලද්දේ නම් (සංඛ්යානය දෙගුණ කරන ලද්දේ නම්) B සමාන ප්රස්ථාරයක් ලැබෙනු ඇත.
මෙසේ ගත කළ කාලය අඩකින් අඩු කළවිට ධාරාව උපරිමයට යාමට අවශ්ය කාලය t1 ගත විමට පෙර ධාරාව විස්නධි කරනු ලබයි. එවිට ධාරාව ඇත්තේ P ලක්ෂ්යයේ වෙයි. ධාරාව විසන්ධි කළ නිසා එය Q හිදි ශුන්ය වෙයි. එවිට ම, විරුද්ධ අතට සන්ධි කරනු ලැබු, ධාරාව, එහි පුර්ණ අගයට ළඟා විමට අවශ්ය කාලය වන t4 අඩක් ගතවත් ම නැවතත්, විසන්ධි කරනු ලබයි. එවිට R ලක්ෂයයේ සිට S ලක්ෂ්ය තෙක් ගලන ධාරාව S හිදි ශුන්ය වෙයි. මෙම ක්රියාවලිය නොනවත්වා කළහොත් OPQRS... වැනි ප්රස්ථාරයක් ලැබෙයි.
මෙහි කරන ලද්දේ එකම පේ්රරකයකට එක සමාන වොල්ටියතාවක් අවස්ථා දෙකෙහි දි සංඛ්යාත දෙකකින් දීම. ප්රථම අවස්ථාවේ දි මෙන් දෙගුණයක සංඛ්යාතයකින් දෙවන අවස්ථාවේ ධාරාව පේ්රරකයට ප්රධානය කරන ලදි. සංඛ්යාතය වැඩිවිම හේතුවෙන් දෙවන අවස්ථාවෙහි දි ධාරාවෙහි උපරිමය වුයේ ප්රථම අවස්ථාන් අඩකි. (I/2) මෙපරිද්දෙන් සංඛ්යාතය පළමු වතාවේ මෙන් සිව් ගුණයක් කරන ලද්දේ නම් ධාරාව 1/4 ක් වන්නට තිබිනි. මෙලෙස සංඛ්යාතය වැඩි කරගෙන යාමෙන් ධාරාව අඩු වෙමින් ගොස් එක් අවස්ථාවක දී එය ශුන්ය කර ළඟා වනු ඇත. ගුවන් විදුලි සංඛ්යාත පේ්රරක සදහා හරය වාතය විම වැදගත් වන්නේ අඩු පේ්රරතාව හේතුවෙනි.
අන්යොන්ය පේ්රරතාව (Lm)
දඟර දෙකක් අතර ඇති වන පේ්රරණය අන්යෝනය පේ්රරතාව වෙයි. 13.6 චිත්රයෙහි එකිනෙක ආසන්නයෙහි දඟර දෙකක් වෙයි. ඉන් එක් දඟරයක් L1 ධාරාවක් ගලන විට. එම දඟරයෙහි ඇති වන චුම්බක රේඛා ආසන්න දඟරයL2 හරහා වැටේ. L1දඟරයෙහි අගය වෙනස් වන ධාරාවක් හෝ ප්රත්යාවර්ත ධාරාවක් ගලන්නේනම් එහි වෙනස් වන චුම්බකතාවය නිසා L2 දඟරයහි විද්යුත්ගාමක බලයක් පේ්රරණය වෙයි. L2 ට භාරයක් R සම්බන්ධ කර අති විට ඒ හරහා ධරාවක් ගලයි.
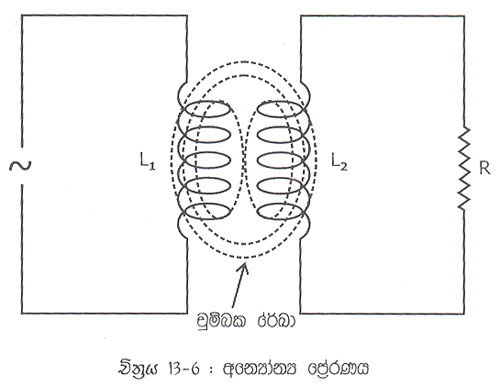
L2 හරහා ගලන පේ්රරිත ධාරිව නිසා L1 හි ද වි. ගා. බලයක් ආපසු පේ්රරණය වෙයි. මෙලෙස දඟර අතර ඇතිවන පේ්රරණයට අනෙන්යා්න්ය පේ්රරතාව යැයි කියනු ලැබේ.
අනෝයා්න්ය පේ්රරනයෙහි එක්කයද හෙන්රි (H) වෙයි අනෝයා්න්ය පේ්රතාව Lm ලෙස කේත ගත කෙරේ.
එක දඟරයක තත්පරයකදී ඇම්පියරය බැගින් ධාරා වෙනසක්වන විට ආසන්නයෙහි ඇති අනේක්් දඟරයෙහි වොල්ටි එකක විද්යුත් ගාමකබලයක් පේ්රරණය වන්නේ නම් දඟර දෙක අතර අන්යෝනය පේ්රතාව හේන්රි එකක් ලෙස සලකනු ලැබේ.
බොහෝ විට දඟර දෙකක් අතර චුම්බක ස්රාවය සම්පුර්ණයෙන් බන්දනය වන්නේ නැත. එවිට ස්රාවය අපතේ යාමක් සිදු වේ. මෙය ස්රාවය කාන්දු විම යැයි හැඳින්වෙයි.
දඟර ඇඳුම
එක දඟරයක් චුම්බක ස්රාවයට අනෙක් දඟරය සම්බන්ධ කර ගැනිම දඟර ඇඳුම වෙයි. එක දඟරයක ඇති වු චුම්බක ස්රාවය තවත් දඟරයකට එක එක් ප්රමාණයක සම්බන්ධ විය හැකිය. ඒ දඟර දෙකෙහි පිහිටිම හර ද්රවය වැනි කරුණු මත රදා පවති. ඇඳුම් සංගුණිකය ලෙස නිර්වචනය කෙරෙන්නේ එක් දඟරයක ඇති ස්රාව ප්රමාණයෙන් කෙතරම් කොටසක් අනෙක් දඟරයට ඇදන්නේ ද යන්නයි.
ආඳුම් සංගුණිකය
k = ප්රථම සහ දෙවන දඟර අතර ස්රාව අඳුම / ප්රථම දඟරයේ ස්රාව ප්රමාණය
මෙය (13.6) චිත්රයට අනුව,
k = L1සමහ L2අතර ස්රාව ඇඳුම / L1හි මුළු ස්රාව ප්රමාණය.................................(13.4)
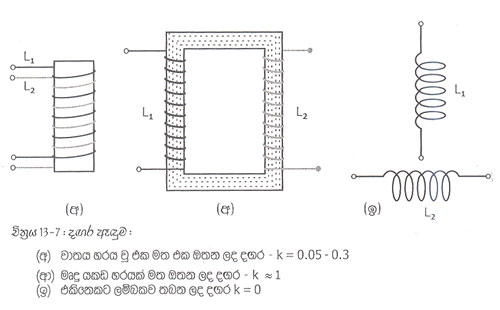
දඟර දෙක ඉතා සමිපව තැබිමේ ඇඳුම සංගුණකය වැඩි වෙයි. බොහෝ විට එක දඟරයක් අනෙක මත ඔතනු ලැබෙයි. එක මෘදු යකඩ හරයක් මත එතුම් දෙකම තිබිමෙන් සහ එකිනෙකට සමාන්තරව තිබිමන් ද k වැඩි අගයක් ගනි. මේ අතර, දගර එකිනෙක සම්බන්ධව තැබිමෙන් ඇඳුම් සංගුණිකය අවම වේ. එක දඟරයක චුම්බක ක්ෂේත්රය අනෙක බලපෑම අවම කිරිමට දඟර එකිනෙකද ලම්බකව තබනු ලැබෙන අඳුම් සංගුණිකය ශුන්ය වු විට දඟර අතර අනෙයා්න්ය පේ්රරණයක් නොවේ.
අඳුම් සංගුණිකයට ඒකක නොමැත. එය දඟර දෙකක් අතර අනුපාතයක් පමණික. දඟර දෙක අතර ඉහල ම ඇදුම ඇති විට ඇඳුම් සංගුණිකය 1 වේ. අඳුම් ලිහිල් වන විට අඳුම් සංගුණිකය 0.05 සිට 0.3 තෙක් පරාසයක පවති. මෙවැනි දඟර දෙකක් අතර ස්රාව අඳුම් 5% සිට 30% දක්වා විය හැක. මේ අතර , මෘදු යකඩ හරයක් මත වු හෝදින් ඇඳු දඟර දෙකක් අතර අඳුම් සංගුණිකය 1 දක්වා ඉහළ යන්නේ ස්රාව ඇඳුම 100% ක් ම වන හෙයිනි.
උදාහරණ 13.3
ප්රාථමික දරඟයෙහි චුම්බක ක්ෂේත්රය 80Wb වෙයි. අඳුම් සංගුණිකය k= 0.75 ද්විතිය දඟරයෙහි ඇඳුම් ස්රාවය කොපමනද?
විසඳුම්
k = L2 හි ඇඳුම් ස්රාවය / L1හි ස්රාවය
L 2හි අඳුම් ස්රාවය = k x L1හි ස්රාවය
=0.75 x 80Wb
=60Wb
L1 සහ L2 මෘදු යකඩ හරයක් මත ඔතන ලද නම් k≈1 නිසා L2 හි ද ස්රාවය 80Wb ට සමිප වනු ඇත.
 ශිල්ප 64
ශිල්ප 64