පේ‍්‍රරතාව සහ හරය



පේ‍්‍රරතාව, දඟරයක හරයෙහි පාරගම්‍යතාව මත වෙනස් වෙයි. පාරගම්‍යතාව මත ස‍්‍රාව ඝන්තවය වෙස් විම මෙයට හේතුවයි. වාතය හරය වු දඟරයක මෙන් සිය ගුණයක් (x100) පමන මෘදු යකඩ හරය වු දඟරයක පේ‍්‍රරතාව වැඩිය.

ගුවන් විදුලි සංඛ්‍යාතය සඳහා වාතය හරය වු දඟරය ද, ශ‍්‍රව්‍ය සංඛ්‍යාත සඳහා මෘදු යකඩ හර ද යොදා ගැනේ, සංඛ්‍යාත අධික ගුවන් විදුලි තරංග සඳහා මෘදු යකඩ හර යොදා ගත හොත් ස්වයං පේ‍්‍රරතාව අධික වීම නිසා ධාරාව ගැලිම සම්පුර්ණයෙන් ඇණ හිටි.

දඟරයක පේ‍්‍රරිත වෝලටීතාව (Vl)



13.2 ෙඡ්දයෙහි දඟරයක පේ‍්‍රරණය වන වෝලටීයතාව (Vl) ගැන සඳහන් කරන ලදි ඒ පිළිබඳ තවත් පැහැදිලි කර ගැනීම ප‍්‍රයෝජනවත්ය.

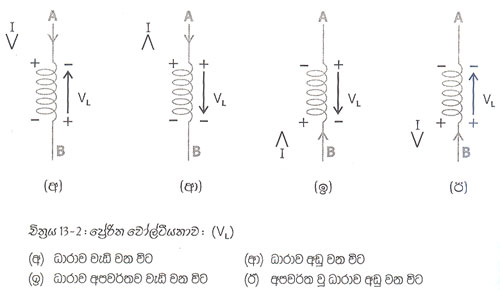
13.2 චිත‍්‍රයෙහි (අ) රූපයෙහි දඟරයේ ධාරාව් A සිට B දක්වා ගැලිමට පටන් ගනි. පළමු පොටෙහි ධාරාව ගලවාත් සමඟ ම චුම්බක කේෂ්ත‍්‍රයක් ඇති විමෙන් දෙවන පොටෙහි විද්‍යුත් ගාමක බලයෙක් ඇති වේ. දෙවන පොටෙහි ධාරාව ගලත්ම තෙවන පොටෙහි ද ආදි වශයෙන් සියළුම පොටවල්වල විද්‍යුත් ගාමක බලයක් පේ‍්‍රරණය වෙයි. මෙසේ පේ‍්‍රරණය වන වී. ගා බලය දඟරයෙහි ධාරාව ගලන දිශාවට ප‍්‍රතිවිරුද්ධ දිශාවට (ලෙන්ස්ගේ නියමය) බලපායි. එහි ප‍්‍රතිඵලය ධාරාව I උපරිමය දක්වා වැඩි විමට වැඩි කාලයක් ගත විමයි.

දෙවන අවස්ථාව (ආ) රූපයෙන් දැක්වයි. මෙහි දී වන්නේ ධාරාව විසන්ධි කිරිමයි. එවිට චුම්භක කේෂ්ත‍්‍රය බිඳ වැටීම සිදුවෙයි. ක‍්‍රම ක‍්‍රමයෙන් චුම්බක රේණා හැකිළෙන විට AB දඟරය හරහා නැවතත් වි. ගා. බලයක් (Vl) පේ‍්‍රරණය වෙයි. ලෙන්ස්ගේ නියමයට අනුව එය සිදුවන්නේ චුම්බක ක්ෂේත‍්‍රය බිඳවැටීම නවත්වන ආකාරයට එනම් ධාරාව විසන්ධි විම නවතින ආකාරයට එසේවිටම ධාරාව නොකඩවා ගැලිය යුතු වේ. එම නිසා (Vl) පේ‍්‍රරණය වන්නේ I ධාරාව ගලන දිශාවටම A සිට B දක්වා මෙලෙස ධාරාව සම්බන්ධ කොට. නැවත විසන්ධි කිරිම් දි AB හරහා ධාරාව ගලන ආකාරය 13.3 චිත‍්‍රයේ ප‍්‍රස්තාරයහි නිරූපණය ෙවි.

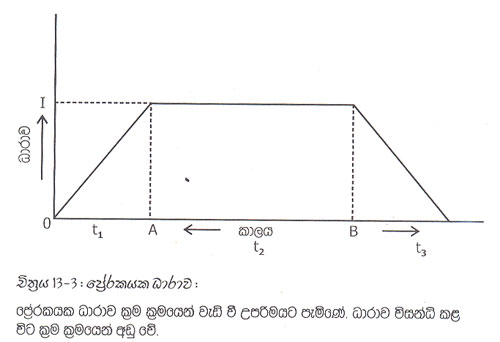
13.3 ප‍්‍රස්තාරයෙහි මුල ලක්ෂ්‍ය (O) ධාරාව පේ‍්‍රරකයට සම්බන්ධ කළ අවස්ථාවයි. ස්වයං පේ‍්‍රරණය නිසා ධාරාව උපරිමයට පැමිණිමට t1 කාලයක් ගත වෙයි. t2 කලායක් තුළ ධාරාවක් නොවෙනස්ව ගලන නිසා වෙයි. ගා. බලයක් පේ‍්‍රරණය වන්නේ නැත. ධාරාව උපරිමයේ පවති. B ලක්ෂයෙහි දී (t1 ,t2 .................කාලයට පසු) ධාරාව විසන්ධි කෙරේ. එහෙත්, ස්වයං පේ‍්‍රරණය නිසා ධාරාව තවදුරටත් ගලයි. ධාරාව ශුන්‍යයට පත්වන්නේ B සිට t3 කාලයක් ගතවු පසුය.

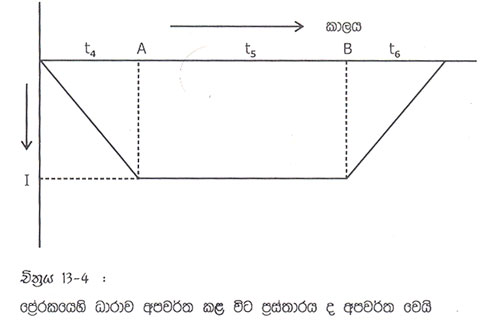
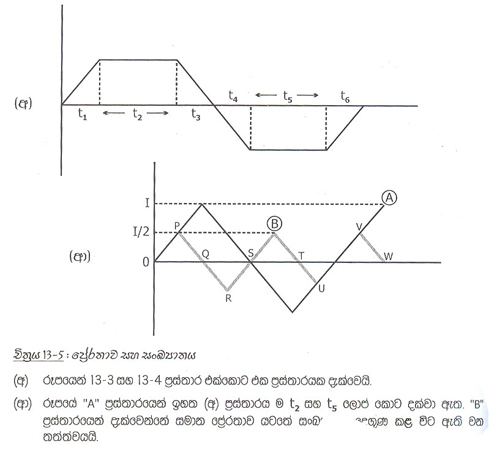
13-2 චිත‍්‍රයේ (ඉ) රූපයෙහි දැක්වෙන්නේ ධාරාව අපවර්ති කොට සම්බන්ධ කරන අවස්ථාවයි. එහිදි සිදුවන්නේ ද (අ) රූපයෙහි දැක්වෙන සිද්ධියේ ම අපවර්ත තත්ත්වයයි. (ඊ) රූපයෙහි ධාරාව විසින්ධි කරන අවස්ථාව නිරූපණය වෙයි. එහි (ආ) රූපයෙහි දැක් වු අවස්ථාව අපවර්ත තත්ත්ව පෙන්නුම් කරයි. මේ (ඉ) සහ (ඊ) රුපවල අවස්ථා ද සඳහා ද 13.3 එවැනි ප‍්‍රස්තාරයක් අඳින ලද්දේ නම්, එය 13.3 ට සම්පේ‍්‍රණයෙන් සමාන වනු ඇත. එකම වෙනස ධාරාව ගලන දිශාව පමණකි. 13.4 චිත‍්‍රය බලන්න.