ධාරාව ගලන දිශාව



ලෙන්ස්ගේ නියමයට අනුව ධාරාව ගන්නේ වෝලටියතා පේ‍්‍රරණයට බාධා ඇතිවන ආකාරයට ය. පේ‍්‍රරණයට බාධා ඇති විමට නම්, භ‍්‍රමණයට බාධා ඇති විය යුතු ය. පුඩුවෙහි C'B' පැත්ත බලන විට, එය ආසන්නයේ ඇත්තේ උත්තර ධ‍්‍රැවයක් නිසා. C'B' චලනයට බාධා කිරිමට එහි දක්ෂිණ ධ‍්‍රැවයක් පේ‍්‍රරණය විය යුතු වෙයි. එවිට කස්කුරුප්පු නියමය හෝ සුරත් නියමය යොදා ගැනිමෙන් ධාරාව C' සිට B' දක්වා ගලන බව පෙනේ. මෙලෙස ම සැලකිමෙන් A'D' පැත්තෙමි ධාරාව A' සිට D' දක්වා ගලන බව සිතාගත හැක. එම නිසා, පුඩුවෙහි පේ‍්‍රරණය වන ධාරාව ක්‍C'B' සහA'D' දෙපැත්තහි ඓක්‍යය වෙයි.

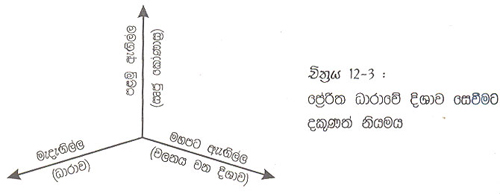
සුරත් නියමය : දකුණතෙහි මහපට ඇඟිල්ල, පළමු ඇඟිල්ල සහ මැදඟිල්ල එකිනෙකට සෘජු කේණාස‍්‍රව තබන්න. මහපට ඇඟිල්ලේන් සන්නායකය චලනය වන දිශාව ද පළමුව ඇඟිල්ලෙන් චුම්බක ක්ෂේත‍්‍රය හිමි දිශාව ද දක්වන විට, මැදඟිල්ල ධාරාව ගලන දිශාව පෙන්වයි.

සන්නායකයක පේ‍්‍රරිත ධාරාව ගලන දිශාව පහසුවෙන් සොයා ගැනිම සඳහා සුරත් නියමය යොදා ගත හැක (චිත‍්‍රය 12.3)

12.3 පේ‍්‍රරිත වෝලටීයතා චක‍්‍රය

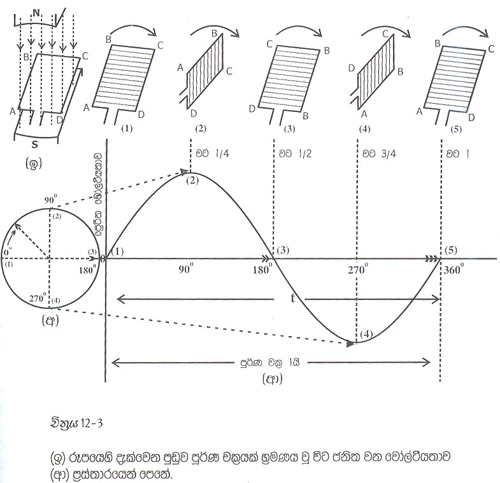
12.2 චිත‍්‍රයේ පුඩුවෙහි එක් අවස්ථාවක පේ‍්‍රරිත වොල්ටීයතාව උපරිමයට නැග, ඉන් 90 ද කට පසු ශුන්‍ය දක්වා අඩුවන සැටි දුටුවෙමු. තවත් 90 ද ක් ගිය තැන නැවතත්, (දිශාව මාරුව) උපරිමය තෙක් වැඩි වන වොල්ටීයතාව, පුඩුව පෙර සිට තැනට එන විට ශුන්‍ය වෙයි. මෙසේ එක් පුර්ණ චක‍්‍රයක් සම්පුර්ණ වන විට වොල්ටීයතා උපරිම දෙකක් සහ අවම දෙකක ද ඇති වේ.

12.2 චිත‍්‍රයට සමාන සෘජුකෝනාස‍්‍ර පුඩුවක් චුම්බක ක්ෂේත‍්‍රයක පුර්ණ වක‍්‍රයක් භ‍්‍රමණය වු විට පේ‍්‍රරණය වන වේලටීයතා සවිස්තරව 12.3 චිත‍්‍රයෙහි වෙයි.

10 වන පරිච්චේදයෙහි සුරත් නියමය යොදා ගැනෙන්නේචුම්බක ක්ෂේත5යෙ ්දිශාව දැක්වීමටය. මෙහි දී එය ධාරාවේ දිශාව පෙන්විටම යෙදේ. මේ දෙකෙහි වෙනස වටහා ගැනිම වැදගත්ය.

එහි (ඉ) රූපයෙහි ABCD පුඩුව (1) අවස්ථාව භ‍්‍රමණය පටන්ගත් අවස්ථාවයි. චුම්බක රේඛාවලට සමාන්තර නිසා වෝල්ටීයතාවක් නොවේ. (1) සිට (2) දක්වා භ‍්‍රමණය වන විට චුම්බක රේඛා ක‍්‍රම ක‍්‍රමයෙන් වැඩි වැඩියෙන් කැපි (2) අවස්ථාවේ දි උපරිම ප‍්‍රමාණයක් කැපේ. මේ අවස්ථාවේ පේ‍්‍රරණය වන වෝල්ටියතාව උපරිම වේ. පුඩුව 90 ද ක් භ‍්‍රමණයව ඇති අතර, පේ‍්‍රරණය වු වෝලටීයතාව (ආ) ප‍්‍රස්තාරයෙහි (2) අවස්ථාවේ දැක්වේ. (2) අවස්ථාවේ සිට 3 අවස්ථාව දක්වා පුඩුව භ‍්‍රමණය වීමේ දී චුම්බක රේඛා කැපෙන ප‍්‍රමාණය අඩු වි (3) අවස්ථාවේ දි එය ශුන්‍ය වේ. (3) අවස්ථාවෙහි පේ‍්‍රරණය වු වෝල්ටීයතාව ද ශුන්‍යය වේ. මේ බව (ආ) ප‍්‍රස්ථාරයෙහි (3) අවස්ථාවෙන් නිරූපණය වෙයි. පුඩුව මේ වන විට 180 ද ක් භ‍්‍රමණය වී ඇත.

(3) අවස්ථාවේ සිට (4) අවස්ථාව දක්වා පුඩුව තවදුරටත් භ‍්‍රමනය වීමේ ද ක‍්‍රම ක‍්‍රමයෙන් නැවතත් චුම්බක රේඛා කැපෙන අතර, (4) අවස්ථාවේ දි එය උපරිමයට පැමිණ, ප්‍රෙරිත වෝලටියතාව ද උපරිමයට පැමිණේ. කෙසේ වෙත් (3) සිට (4) දක්වා භ‍්‍රමණය වෙද්දි ධාරාව ප‍්‍රතිවිරුද්ධ දෙසට ගලන්නට පටන් ගනි. (ආ) ප‍්‍රස්තාරයේ (3) සිට (4) දක්වා භ‍්‍රමණය වෙද්දි ධාරාව ප‍්‍රතිවිරුද්ධ දෙසට ගලන්නට පටන්ගනි. (ආ) ප‍්‍රස්තාරයෙහි (3) සිට (4) දක්වා ඝෘණ අගය වැඩි වන්න් එහෙයිනි. (4) වන අවස්ථාව වන විට පුඩුව 270ද ක් සම්පුර්ණ කර සිටි, මෙය (අ) රුපයෙන් පෙන්නුම් කරයි.

(4) අවස්ථාවේ සිට (5) අවස්ථාව දක්වා නැවතත් ක‍්‍රම ක‍්‍රමයෙන් වෝල්ටීයතා පේ‍්‍රරණය අඩු වි (5) අවස්ථාවේ දී ශුන්‍යය වේ. මේ වනවිට පුඩුව 360ද ක් භ‍්‍රමණයව ප‍්‍රස්ථාරය බලන්න. (ආ) ප‍්‍රස්තාරයෙහි (1) සිට (5) දක්වා නිරුපණය වන්නේ ප‍්‍රත්‍යවර්ත වෝලටීයතා පුර්ණ චක‍්‍රයකි. දඟරයක් චුම්බක ක්ෂේත‍්‍රයක භ‍්‍රමණය වන විට මෙවැනි ප‍්‍රත්‍යාවර්ත වෝලටියතාවක් එහි පේ‍්‍රරණය වේ. (අ) ප‍්‍රස්තාරයෙහි දැක්වෙන තරංගය හඳුන්වනු ලබන්නේ සයිනාකාර තරංගයක් ලෙසය. අප නිවෙස්වලට විදුලිය සැපයෙන ජාතික විදුලි බල පද්ධතියෙන් ලැබෙන්නේ ද සයිනාකාර ජව සැපයුමකි.