ශ්‍රේණිගත - සමාන්තරගත පරිපථයක සමස්ත ප‍්‍රතිරෝධය

8.2 චිත‍්‍රයේ පරිපථයෙහි ප‍්‍රතිරෝධක 4 ක් ශ්‍රේණිගත - සමාන්තරගත ක‍්‍රමයට අමුණා ඇතිය අයුුරු පෙනෙයි. R1සහ R2සමාන්තරගත කොට R1සහ R2 සමඟ ශ්‍රේනිගතව සම්බන්ධ කර ඇත.

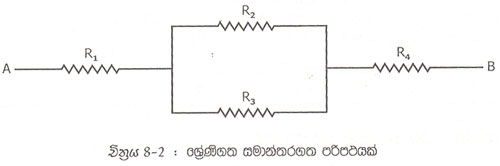
අවශ්‍ය නම් ඕම් මානය පාවිච්චි කොට මෙම පරිපථයේ A සිට B දක්වා වු මුළු ප‍්‍රතිරෝධය මැන ගත හැක. එහෙත්, මෙහි දි අවශ්‍ය වන්නේ පරිපථයේ සමස්ත ප‍්‍රතිරෝධය සඳහා සුත‍්‍රයක් සොයා ගැනිමය.

8.2 පරිපථයෙහි R2 සහ R3 සමාන්තරව ඇති නිසා එහි සමක ප‍්‍රතිරෝධය සෙවිය හැක. (7 වන පරිච්ෙඡ්දය) මෙම සමක ප‍්‍රතිරෝධය Rt වේ යැයි සිතමු. එවිට මේ පරිපථයක ප‍්‍රතිරෝධක 3 ක් ශ්‍රේණිගත කළ ලෙස දැක්විය හැකිය.

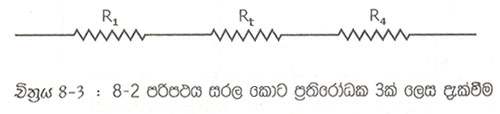
මෙසේ සරල ලෙස 8.2 පරිපථය 8.3 චිත‍්‍රයෙහි දැක්වයි. 8.3 චිත‍්‍රයේ පරිපථයෙහි මුළු ප‍්‍රතිරෝධය සෙවිම ඉතා පහසුය.

RT = R1 +RT +R4

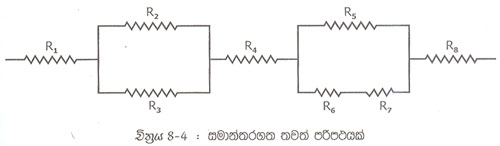
8.4 චිත‍්‍රයෙි තවත් ශ්‍රේණිගත සමාන්තරගත පරිපථයක් වෙයි. 8.2 චිත‍්‍රයෙහි පරිපථය විසඳු ක‍්‍රමයට ම මෙය ද විසඳිය හැක. මෙහි R6 සහ R7 ශ්‍රේණිගත කොට ඇති නිසා ඒ දෙක එකතු කොට R6T (R6T =R6 +R7)

ලෙස දැක්වමු. එවිට 8.5 චිත‍්‍රයේ පරිපථය ලබයි.

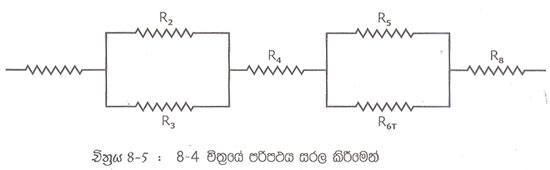
8.5 චිත‍්‍රයේ පරිපථයෙහි R2 සහ R3 සමක ප‍්‍රතිරෝධය Rt1ලෙස ද, R5 සහ R6 සමක ප‍්‍රතිරෝධය Rt2 ලෙස ද දැක්විය හැක. එවිට ලැබෙන පරිපථය 8.6 චිත‍්‍රයේ දිස්වෙයි.

8.6 චිත‍්‍රයේ පරිපථයෙහි සමස්ත ප‍්‍රතිරෝධය



RT = R1 +RT1 +RT1 +R4 +RT4 R8

එම නිසා, 8.4 චිත‍්‍රයේ පරිපථයෙහි සමස්ත ප‍්‍රතිරෝධය ඉහත සමීකරණයෙන් දැක්වෙයි.

ඉහත ආකාරයට ශාඛා ප‍්‍රතිරෝධ වෙන වෙනම විසඳා මුළු පරිපථයම වඩා සරල පරිපථයක් බවට පත්කර ගැනිමෙන් පරිපථයෙහි මුළු ප‍්‍රතිරෝදය සොයා ගැනීමට පහසු වෙයි.

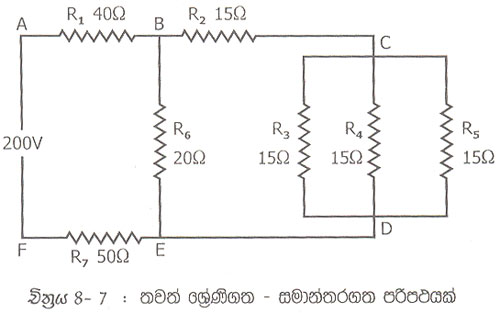
උදාහරණ 8.1



8.7 චිත‍්‍රයේ දැක්වන පරිපථයෙහි සමක ප‍්‍රතිරෝධය සහ මුළු ධාරාව ද, ශාඛා ධාරාව සහ වෝලටීයතා ද වෙන වෙන ම සොයන්න.

විසඳුම



මෙම පරිපථයෙහි වෝලටීයතා ජනකයෙන් දුර කෙරවෙලෙහි සිට සමක ප‍්‍රතිරෝධය සෙවිම පහසුය. ප‍්‍රථමයෙන් R3 R4 සහ R5 හි සමක ප‍්‍රතිරෝධය සොයමු.

1/RT1 =1/15 + 1/15 + 1/15

RT1 =5Ω



මේ නිසා R3 R4 සහ R5 වෙනුවට 5Ω අගයක් ඇති එක ප‍්‍රතිරෝධකයක් යෙදිය හැක. නව පරිපථය 8.7 චිත‍්‍රයෙහි දැක්වේ.

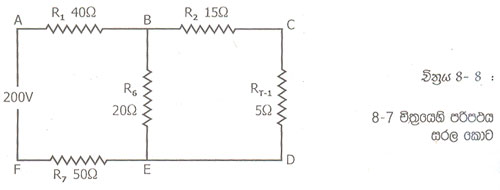
8.7 චිත‍්‍රයෙහි Rt-1 සමඟ R2 ශ්‍රේණිගත කොට ඇත. මේ දෙකෙහි සමක ප‍්‍රතිරෝධය Rt-2=20Ω කි.

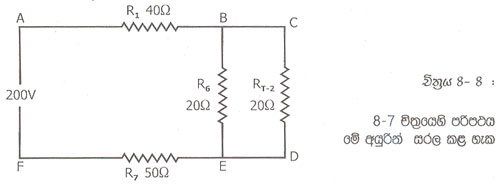
8.8 චිත‍්‍රයෙහි Rt-2 සහ R6 සමාන්තරගතව තිබේ. මෙම ප‍්‍රතිරෝධක වෙනුවට 10Ω ක ප‍්‍රතිරෝධකයක් ආදේශ කළ හැක. එම ප‍්‍රතිරෝධකය Rt3 වශයෙන් යොදා අවසාන පරිපථය 8.9 චිත‍්‍රයෙහි නිරූපණය වෙයි.

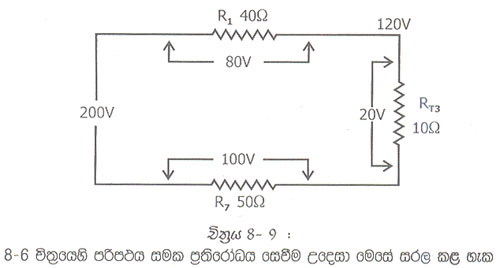
8.6 චිත‍්‍රයෙහි පරිපථයෙහි සමක ප‍්‍රතිරෝධය, චිත‍්‍රයේ පරිපථයෙන් පහසුවෙන් සෙවිය හැක.

RT = R1 +RT3 +R2

RT = 40 Ω +10 Ω +50 Ω

= 100 Ω



සමක ප‍්‍රතිරෝධය 100Ω කි.



මුළු ධාරව = 200V / 100 W = 2A

8.6 චිත‍්‍රයේ පරිපථ දෙස නැවත නෙත් යොමු කළ විට, R1 හරහා මුළු ධාරාව ම ගලයි.

R1 විභව පාතනය R = 40X2 =89V

A ට වඩා B-80V ක විභව පාතනයක සිටී. එහෙයින් B වල වොල්ටීයතාව 120 V(200V-8-V) (8.10 චිත‍්‍රය බලන්න)

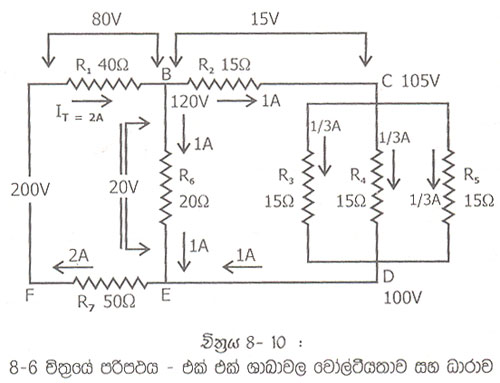
R2 ලR3 ලR4සහ R5 සමක ප‍්‍රතිරෝධය (Rt2), R6 ප‍්‍රතිරෝධයට සමාන නිසා (චිත‍්‍රය 8- 8) මුළු ධාරාව මෙම ප‍්‍රතරෝධක දෙකෙහි සමව බෙදයි. එවිට R6 හරහා ධාරාව 1A වේ. R6 හරහා විභව පාතනය 20V වෙයි. අනෙක් 1A ධාරාව R2 හරහා යන නිසා R2 හි විභව පාතනය 15V කි. මේ නිසා C ‍හි වෝලටියතාව 105V(120V – 15V) කි.

C සිට D දක්වා සමාන්තරගතව ඇති R3 R4සහ R5 එක සමාන අගයකින් යුත් නිසා 1A ධාරාව තුනට බෙදේ.

එවිට ඉන් එක ප‍්‍රතිරෝධකයක් තුලින් ගන්නේ 1/3A ධාරාවකි. එහෙයින් C සිට D දක්වා විභව පාතනය (15 X 1/3)5V වෙයි D හි වොල්ටීයතාව (105-5) 100V වෙයි. මෙය E හි වොල්ටීයතාව ද වේ. R6 හි විභව පාතනය ගෙන බැලූ විට ද E හි ඇත්තේ (120 – 20) 100V කි. ඉන් පෙනෙන්නේ පරිපථ විශ්ලේෂණය නිවැරදි බවය.

E සන්ධියේදී D සිට එන ධාරාවත්, B සිට R6 හරහා එන ධාරාවන් එකතුවී මුළු ධාරාව 2Aවේ. එහෙයින් R7 තුළින් 2A ධාරාවක් ගලයි. R7 හරහා විභව පාතනය 100V (50 x 2) ක් වෙයි. E වල වෝල්ටීයතාව වන 100 V, F‍ වලදී ශුන්‍යයට බසි. F‍ වෝල්ටියතාව ජනකයේ ඝෘණ අග‍්‍රයයි.