A Panasonic televsion (model CT-27D31) has a 27-in screen.  The "aspect-ratio" (length to width) for most standard TV screens is 4:3.  Find the length and width (height) for this model television.

 

High-definition televisions, with a wide-screen format, are manufactured with an aspect-ratio (length to width) of 16:9.  Find the length and width (height) of a 27" model television with the HDTV's wide-screen format?

 

Grade is defined as the ratio of the change in elevation (or vertical distance) to the change in horizontal distance. If a ¾-mi stretch of road has an average 8% grade, then what is the corresponding change in elevation over this distance.  Express the answer rounded to the nearest whole number of feet.

 

The pilot of a commerical airliner determines that his plane is 75 miles from Hilo Airport at an altitude of 10,000 feet.

1. What (horizontal) distance along the surface is the plane from the airport?
2. If the pilot maintains a constant descent rate of 500 feet per minute (fpm), at what speed should the plane be flown to land at the airport.  Hint: first find the time it takes to descend 10,000 ft.

 

High-capacity recordable CD's (a.k.a. CD-R's) are often sold in 10-packs.  The advertisement shown (at right) shows them on sale at a package price of $3.99.  If each (high-capacity) CD can hold 700 MB of data, find the unit price in cents per gigabyte.
 

Below are measurements for two of the more common storage mediums for present-day pc's (personal computers). A magnetic (double-density) floppy disk's storage capacity is 1.44 MB while a standard (optical) compact disc, or CD, has a storage capacity of 650 MB.  

1. Determine the storage capacity density (storage capacity per unit area) for a magnetic floppy disk.  Note that floppy disks are double-sided and thus they utilize both sides of the magnetic disk for data storage.
2. Determine the storage capacity density for a standard CD.
3. How many times greater is a standard CD's storage capacity density than that of a magnetic floppy disk?

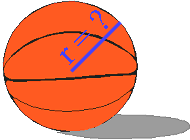
Measure the circumference of a regulation (conventional) basketball and calculate a value for the radius.  Round the answer to the nearest hundredth of an inch.   
Use the result of the previous exercise (#7)
above for exercises #8 - 10, below...  
 

Mt. Everest (in Asia) extends up to an elevation of 29,035 ft while the Mariana Trench reaches down to a depth of 36,201 ft.  If the Earth were scaled down to the size of a basketball, how high and how deep would Mt. Everest and the Mariana Trench, respectively, be?  Express the answer in millimeters.

 

If the Sun (radius = 432,475 miles) were scaled down to the size of a basketball, then how large would the Earth’s diameter be?  Express the answer in millimeters.

 

If the Sun were scaled down to the size of a basketball as in the previous exercise (see #9 above), then how far should it be separated from the Earth in order to represent the actual (average) distance of approximately 93 million miles?  Express the answer in feet.

 

Determine how far one can see to the horizon, assuming that the human eye is 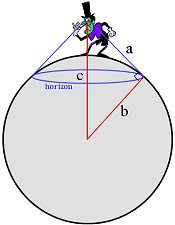5½ ft above the ground (and that there are not any obstructions in your field of view), when standing on:

1. the ground.
2. a ten foot tall platform.

Caution: you will most likely need to retain several decimal places (5 or more) throughout your calculations in order to obtain a reasonable result...

Show that the formula given by, d =miles, approximates the distance to the horizon, where h represents the height (feet) of the observer’s eye above the ground, whenever h is relatively small.