

 |
 |
 |
| 1/2 | 1/4 | 3/8 |
|
(One-Half)
|
(One-Quarter)
|
(Three-Eighths)
|
| The top number tells how many slices you have and the bottom number tells how many slices the pizza was cut into. | ||
We call the top number the Numerator, it is the
number of parts you have.
We call the bottom number the Denominator, it is the number of parts the
whole is divided into.
| Numerator |
| Denominator |
You just have to remember those names! (If you forget just think "Down"-ominator)
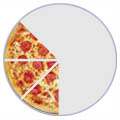
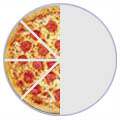
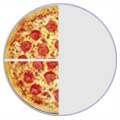
| 4/8 | = | 2/4 | = | 1/2 |
| (Four-Eighths) | Two-Quarters) | (One-Half) | ||
 |
 |
 |
You can add fractions easily if the bottom number (the denominator) is the same:
| 1/4 | + | 1/4 | = | 2/4 | = | 1/2 |
| (One-Quarter) | (One-Quarter) | (Two-Quarters) | (One-Half) | |||
 |
 |
 |
 |
Another example:
| 5/8 | + | 1/8 | = | 6/8 | = | 3/4 |
 |
 |
 |
 |
| 3/8 | + | 1/4 | = | ? |
 |
 |
 |
| 3/8 | + | 2/8 | = | 5/8 |
 |
 |
 |
Equivalent Fractions have the same value, even though they may look different.
These fractions are really the same:| 1 | = | 2 | = | 4 |
| 2 | 4 | 8 |
So, here is why those fractions are really the same:
| × 2 | × 2 | |||
|
|
||||
| 1 | = | 2 | = | 4 |
| 2 | 4 | 8 | ||
|
|
||||
| × 2 | × 2 | |||
| 1/2 | 2/4 | 4/8 | ||
 |
= |  |
= |  |
Here are some more equivalent fractions, this time by dividing:
| ÷ 3 | ÷ 6 | |||
|
|
||||
| 18 | = | 6 | = | 1 |
| 36 | 12 | 2 | ||
|
|
||||
| ÷ 3 | ÷ 6 | |||
 |
 |
 |
| 1/2 | 1/4 | 3/8 |
|
(One-Half)
|
(One-Quarter)
|
(Three-Eighths)
|
Converting Mixed Fractions to Improper FractionsTo convert a mixed fraction to an improper fraction, follow these steps:
|