Information
Contents
Information and Non-equilibrium
An Example
Mathematical Formulation
Information and Order
The information content in a given sequence of units be they letters in a sentence, or nucleotides in DNA, depends on the minimum number of instructions needed to specify or describe the structure. Many instructions are needed to specify a complex, information-bearing structure such as DNA. Only a few instructions are need to specify an ordered structure such as a crystal. In this case we have a description of the initial sequence or unit arrangement which is then repeated ad infinitum according to the packing instructions.
A system would be most probably in an equilibrium state (maximum randomness) when leaves to its own devices.
- In static configuration, it is the un-organized arrangement of books in library, for example.
- In thermodynamics, it is the distribution of particles in the most probable state (maximum entropy).
- In atom/molecule, it is the ground state (with minimum energy) for the electrons/atoms.
- In DNA, it is the random arrangement of the bases (which produces un-viable protein for the organism).
Pre-requisites for Information:
- There should be a number of available states.
- In static configuration, it is the different arrangement of books in library, for example.
- In thermodynamics, it is the distribution of particles in phase space (composed of position and velocity).
- In atom/molecule, it is the energy levels for the electrons.
- In DNA, it is the different arrangement of the bases.
There should be a set of rules/process to arrange the system in a particular state (away from equilibrium).
- In static configuration, it is the rules of cataloging in the library. External energy is required for the arrangement.
- In thermodynamics, it is the external energy that re-arranges the system to a non-equilibrium state.
- In atom/molecule, it is again the external energy that excites the electron(s)/atom(s) to higher energy level.
- In DNA, the rules is to arrange the codons (sequence of three bases) for the production of a particular protein.
There is a mean (a way) to execute the rules/process.
- In static configuration, a librarian will be able to complete the task, for example.
- In thermodynamics, an electrical motor will usually do the trick.
- In atom/molecule, the photosynthesis process will collect sun-light to produce molecule in higher energy state.
- In DNA, it is via natural selection (the ribosome will translate the code to protein).
The resulting state is considered to be informative/useful.
- In static configuration, it provides a definite location for the book, for example.
- In thermodynamics, it can produce refrigeration in a box, for example.
- In atom/molecule, it can produce high energy molecule such as ATP for metabolism.
- In DNA, all processes of life depend on its coding.
[Top]
Let us consider the example of finding a book in the library. If someone goes into a large library to borrow a copy of War and Peace, it will take only a few minutes to find the book when the library is in a good state of order. The book will be on the fiction shelves and the author's name will appear in alphabetical order. In the catalogue, the book is given a unique decimal number. There is only one possible way in which War and Peace can be arranged in relation to all the other books. Indeed, there is only one possible way in which the contents of the entire library can be arranged. But then imagine a second library, in which by some quirk of the rules books are arranged on the shelves according to the color of their bindings. There may be a thousand red books grouped together in one section of the shelves. This arrangement contains a certain amount of order and conveys some information, but not as much as in the first library. Since there are no rules governing the ordering of books on the shelves by title and author within the red section, the number of possible ways of arranging the books there is much greater. If the borrower knows that War and Peace has a red binding, he will proceed to the right section, but then he will have to examine each book in turn until he chances upon the one he is looking for. Then imagine a third library, in which all the rules have broken down. The books are strewn at random on any shelf. War and Peace could be anywhere in the building. There is no denying that the books are in a certain specific sequence, but the sequence is a "noise," not a message. It is only one of a truly immense number of possible ways of arranging the books, and there is no telling which one, because all are equally probable. A borrower's ignorance of the actual arrangement is great in proportion to the quantity of these possible, equally probable ways.
[Top]
To quantify the concept of information, let us consider a simple linear array, like the deck of eight cards or the chain of eight amino acids (see Figure).
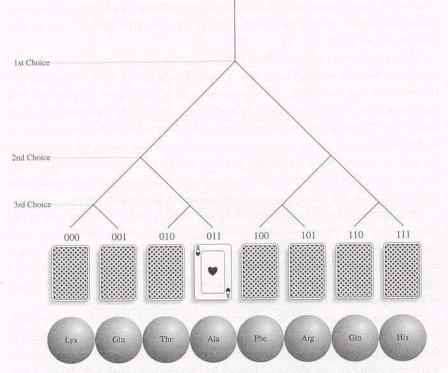
How much information would be needed to locate a particular member in such an array with a perfectly shuffled set? With the cards, the problem is like finding out in a binary guessing game when they are turned face down. Let's start, for example, with the Ace of Hearts. We are allowed in such a binary game to ask someone who knows where the Ace is a series of questions that can be answered "yes" or "no" - a game where the question "Is it here?" is repeated as often as needed. Guessing randomly would eventually get us there; there are eight possibilities for drawing a first card. But, on the average, we would do better if we asked the question for successive subdivisions of the deck - first for subsets of four card, then of two, and finally of one. This way, we would hit upon the Ace in three steps, regardless where it happens to be. The "yes" or "no" are the constraints (the rules). Thus, 3 is the minimum number of correct binary choices or, by our definition above, the amount of information needed to locate a card in this particular arrangement. In effect, what we have been doing here is taking the binary logarithm of the number of possibilities (N=8), i.e., log2(8) = 3. In other words, the information required to determine the location in a deck of 8 cards is 3 bits.
In general, for any number of possibilities (N), the information (I) for specifying a member in such a linear array, is given by
I = log2(1/N).
I here has a negative sign for any N larger than 1, denoting that it is information that has to be acquired in order to make a correct choice.
For the case where the N choices are subdivided into subsets/partitions ( i ) of uniform size (ni), like the four suits in a complete deck of cards. Then the information needed to specify the membership in a partition is again given by
Ii = log2(ni/N) = log2(pi) where pi = ni/N is the probability of finding the member in the partition.
For N = 8, the different value of ni/N and I associated with different partition size are shown in the table below:
i 1 2 4 8
ni 8 4 2 1
ni/N 1 ½ ¼ 1/8
Ii 0 -1 -2 -3
For i = 1, all the members are distributed randomly in one partition, finding the member there is certain but difficult without any information (no rule); while for i = 8, the members are distributed orderly in eight equal size partitions, the chance of finding the member in each is 1/8 and 3 bits of information is required to find the member.
If the partitions are non-uniform in size, then the mean information is given by summing over all the partitions:
I = 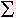 (pi) log2(pi) ---------- (1).
(pi) log2(pi) ---------- (1).
Thus, for N = 8; i = 1,2, ni = 2; i = 3, ni =4; I = 2x(¼)x(-2) + (1/2)x(-1) = -3/2.
The information I is referred to as logical entropy. It is the constraints (rules), which impose the order (creating the information) in the static configuration. The process of re-arrangement will generate entropy (to the external environment) so that the second law of thermodynamic would not be violated.
There is a definition for the measurement of disorder called thermodynamic entropy: All systems tend to become more disorder with the progression of time. Energy is required to re-arrange the system back to a more orderly state - a non-equilibrium state. The Boltzmann equation for entropy is expressed as:
S = -k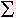 (pi) ln(pi) ---------- (2).
(pi) ln(pi) ---------- (2).
where k = 1.38 x 10(-23) joule/K = 8.617 x 10(-5) ev/K is the Boltzmann's constant and pi = exp(-Ei/kT)/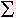 exp(-Ei/kT) is the probability of finding the particle in state i, and ln is logarithm with base e = 2.71828.
exp(-Ei/kT) is the probability of finding the particle in state i, and ln is logarithm with base e = 2.71828.
Entropy, in its deep sense brought to light by Ludwig Boltzmann, is a measure of the dispersal of energy - in a sense, a measure of disorder, just as information is a measure of order. Any thing that is so thoroughly defined that it can be put together only in one or a few ways is perceived as orderly. Any thing that can be reproduced in thousands or millions of different but entirely equivalent ways is perceived as disorderly. Information thus becomes a concept equivalent to entropy, and any system can be described in terms of one or the other. An increase of entropy implies a decrease of information, and vice versa. A mathematical relationship can be obtained by equating the summation in Eq. (1) and (2):
S = -(k ln2) I, or S + (k ln2) I = 0 ---------- (3).
[Top]
Only in terms of information (or entropy) does "order" acquire scientific meaning. We have some intuitive notion of orderliness - we can often see at a glance whether a structure is orderly or disorderly - but this doesn't go beyound rather simple architectural or functional periodicities. That intuition breaks down as we deal with macromolecules, like DNA, RNA, or proteins. Considered individually (out of species context), these are largely aperiodic structures, yet their specifications require immense amounts of information because of their low (pi)s. In paradoxical contrast, a periodic structure - say, a synthetic stretch of DNA encoding nothing but prolines - may immediately strike us a orderly, though it demands a relatively modest amount of information (and is described by a simple algorithm). In other word, INFORMATION ~ ORDER ~ IMPROBABILITY (of realizing the particular order/structure/state) - higher order is more improbable and requires more information to achieve. An orderly system tends to become more disorder with the progress of time. It can be used to define the arrow of time.
The time's arrow of thermodynamic events holds for living as well as nonliving matter. Living beings continuously lose information and would sink to thermodynamic equilibrium just as surely as nonliving systems do. There is only on way to keep a system from sinking to equilibrium: to infuse new information. Organisms manage to stay the sinking a little by linking their molecular building blocks with bonds that don't come easily apart. However, this only delays their decay, but doesn't stop it. No chemical bond can resist the continuous thermal jostling of molecules forever. Thus, to maintain its highly ordered state, an organism must continuously pump in information. The organism takes information from the environment and funnels it inside. By virtue of Eq. (3), this means that the environment must undergo an equivalent increase in thermodynamic entropy; for every bit of information the organism gains, the entropy in the external environment must rise by a corresponding amount.

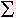 (pi) log2(pi) ---------- (1).
(pi) log2(pi) ---------- (1).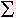 (pi) ln(pi) ---------- (2).
(pi) ln(pi) ---------- (2). 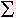 exp(-Ei/kT) is the probability of finding the particle in state i, and ln is logarithm with base e = 2.71828.
exp(-Ei/kT) is the probability of finding the particle in state i, and ln is logarithm with base e = 2.71828.